Electron. J. Differential Equations,
Vol. 2019 (2019), No. 23, pp. 1-19.
Bound states of the discrete Schrodinger equation with
compactly supported potentials
Tuncay Aktosun, Abdon E. Choque-Rivero, Vassilis G. Papanicolaou
Abstract:
The discrete Schrodinger operator is considered on the half-line
lattice
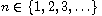 with the Dirichlet boundary condition at
with the Dirichlet boundary condition at
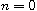 .
It is assumed that the potential
belongs to class
.
It is assumed that the potential
belongs to class
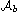 ,
i.e. it is real valued, vanishes
when n>b with b being a fixed positive integer, and is nonzero
at n=b. The proof is provided to show that the corresponding
number of bound states, N, must satisfy the inequalities
,
i.e. it is real valued, vanishes
when n>b with b being a fixed positive integer, and is nonzero
at n=b. The proof is provided to show that the corresponding
number of bound states, N, must satisfy the inequalities
 .
It is shown that for each fixed nonnegative integer k in the
set
.
It is shown that for each fixed nonnegative integer k in the
set
 ,
there exist infinitely many potentials in class
,
there exist infinitely many potentials in class
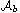 for which the corresponding Schrodinger
operator has exactly k bound states. Some auxiliary results are
presented to relate the number of bound states to the number of real
resonances associated with the corresponding Schrodinger operator.
The theory presented is illustrated with some explicit examples.
for which the corresponding Schrodinger
operator has exactly k bound states. Some auxiliary results are
presented to relate the number of bound states to the number of real
resonances associated with the corresponding Schrodinger operator.
The theory presented is illustrated with some explicit examples.
Submitted December 16, 2018. Published February 11, 2019.
Math Subject Classifications: 39A70, 47B39, 81U15, 34A33.
Key Words: Discrete Schrodinger operator; half-line lattice; bound states;
resonances; compactly-supported potential; number of bound states.
Show me the PDF file (310 KB),
TEX file for this article.
 |
Tuncay Aktosun
Department of Mathematics
University of Texas at Arlington
Arlington, TX 76019-0408, USA
email: aktosun@uta.edu
|
|---|
 |
Abdon E. Choque-Rivero
Instituto de Física y Matemáticas
Universidad Michoacana de San Nicolás de Hidalgo
Ciudad Universitaria, C.P. 58048
Morelia, Michoacán, México
email: abdon@ifm.umich.mx
|
|---|
 |
Vassilis G. Papanicolaou
Department of Mathematics
National Technical University of Athens
Zografou Campus, 157 80
Athens, Greece
email: papanico@math.ntua.gr
|
|---|
Return to the EJDE web page
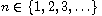 with the Dirichlet boundary condition at
with the Dirichlet boundary condition at
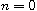 .
It is assumed that the potential
belongs to class
.
It is assumed that the potential
belongs to class
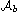 ,
i.e. it is real valued, vanishes
when n>b with b being a fixed positive integer, and is nonzero
at n=b. The proof is provided to show that the corresponding
number of bound states, N, must satisfy the inequalities
,
i.e. it is real valued, vanishes
when n>b with b being a fixed positive integer, and is nonzero
at n=b. The proof is provided to show that the corresponding
number of bound states, N, must satisfy the inequalities
 .
It is shown that for each fixed nonnegative integer k in the
set
.
It is shown that for each fixed nonnegative integer k in the
set
 ,
there exist infinitely many potentials in class
,
there exist infinitely many potentials in class
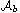 for which the corresponding Schrodinger
operator has exactly k bound states. Some auxiliary results are
presented to relate the number of bound states to the number of real
resonances associated with the corresponding Schrodinger operator.
The theory presented is illustrated with some explicit examples.
for which the corresponding Schrodinger
operator has exactly k bound states. Some auxiliary results are
presented to relate the number of bound states to the number of real
resonances associated with the corresponding Schrodinger operator.
The theory presented is illustrated with some explicit examples.


