Electron. J. Differential Equations,
Vol. 2019 (2019), No. 24, pp. 1-22.
Multiplicity and concentration of positive solutions for fractional
nonlinear Schrodinger equations with critical growth
Xudong Shang, Jihui Zhang
Abstract:
In this article we consider the multiplicity and concentration
behavior of positive solutions for the fractional
nonlinear Schrodinger equation
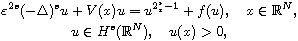
where
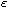 is a positive parameter,
is a positive parameter,
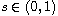 ,
N >2s
and
,
N >2s
and
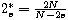 is the fractional critical
exponent, and f is a
is the fractional critical
exponent, and f is a
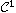 function satisfying
suitable assumptions. We assume that the potential
function satisfying
suitable assumptions. We assume that the potential
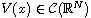 satisfies
satisfies
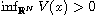 , and that there exits k points
, and that there exits k points
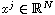 such that for each j=1,...,k,
such that for each j=1,...,k,
 are strictly global minimum. By using the variational method,
we show that there are at least k positive solutions for a small
are strictly global minimum. By using the variational method,
we show that there are at least k positive solutions for a small
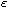 >0.
Moreover, we establish the concentration
property of solutions as
>0.
Moreover, we establish the concentration
property of solutions as
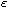 tends to zero.
tends to zero.
Submitted March 10, 2017. Published February 12, 2019.
Math Subject Classifications: 35A15, 58E05.
Key Words: Fractional Schrodinger equations; multiplicity of solutions;
critical growth; variational method.
Show me the PDF file (346 KB),
TEX file for this article.
 |
Xudong Shang
School of Mathematics
Nanjing Normal University
Taizhou College
225300, Jiangsu, China
email: xudong-shang@163.com
|
|---|
 |
Jihui Zhang
Jiangsu Key Laboratory for NSLSCS
School of Mathematical Sciences
Nanjing Normal University
Nanjing 210023, China
email: zhangjihui@njnu.edu.cn
|
|---|
Return to the EJDE web page
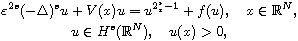
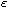 is a positive parameter,
is a positive parameter,
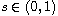 ,
N >2s
and
,
N >2s
and
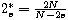 is the fractional critical
exponent, and f is a
is the fractional critical
exponent, and f is a
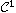 function satisfying
suitable assumptions. We assume that the potential
function satisfying
suitable assumptions. We assume that the potential
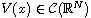 satisfies
satisfies
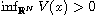 , and that there exits k points
, and that there exits k points
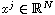 such that for each j=1,...,k,
such that for each j=1,...,k,
 are strictly global minimum. By using the variational method,
we show that there are at least k positive solutions for a small
are strictly global minimum. By using the variational method,
we show that there are at least k positive solutions for a small
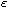 >0.
Moreover, we establish the concentration
property of solutions as
>0.
Moreover, we establish the concentration
property of solutions as
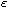 tends to zero.
tends to zero.

