Electron. J. Differential Equations,
Vol. 2019 (2019), No. 26, pp. 1-28.
Differential inclusion for the evolution p(x)-Laplacian with memory
Stanislav Antontsev, Sergey Shmarev, Jacson Simsen, Mariza Stefanello Simsen
Abstract:
We consider the evolution differential inclusion for a nonlocal
operator that involves p(x)-Laplacian,

where
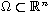 ,
,
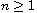 ,
is a bounded
domain with Lipschitz-continuous boundary. The exponent p(x) is
a given measurable function,
,
is a bounded
domain with Lipschitz-continuous boundary. The exponent p(x) is
a given measurable function,
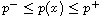 a.e. in
a.e. in
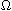 for some bounded constants
for some bounded constants
 and
and
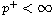 .
It is assumed that
.
It is assumed that
 ,
and that the multivalued function
,
and that the multivalued function
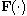 is globally Lipschitz, has convex closed values and
is globally Lipschitz, has convex closed values and
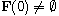 . We prove that the homogeneous
Dirichlet problem has a local in time weak solution. Also we show that
when
. We prove that the homogeneous
Dirichlet problem has a local in time weak solution. Also we show that
when
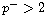 and
and
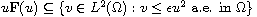 with a sufficiently small
with a sufficiently small
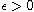 the weak solution possesses
the property of finite speed of propagation of disturbances from
the initial data and may exhibit the waiting time property.
Estimates on the evolution of the null-set of the solution are
presented.
the weak solution possesses
the property of finite speed of propagation of disturbances from
the initial data and may exhibit the waiting time property.
Estimates on the evolution of the null-set of the solution are
presented.
Submitted June 20, 2018. Published February 13, 2019.
Math Subject Classifications: 35R70, 35B99, 35K92, 45K05.
Key Words: Evolution p(x)-Laplacian; nonlocal equation; differential inclusion;
finite speed of propagation; waiting time.
Show me the PDF file (403 KB),
TEX file for this article.
 |
Stanislav Antontsev
CMAF-CIO, University of Lisbon
Lisbon, Portugal.
email: antontsevsn@mail.ru
|
|---|
 |
Sergey Shmarev
Department of Mathematics
University of Oviedo
c/Calvo Sotelo s/n, 33007
Oviedo, Spain
email: shmarev@uniovi.es
|
|---|
 |
Jacson Simsen
Instituto de Matemática e Computação
Universidade Federal de Itajubá, Av. BPS n.1303
Bairro Pinheirinho, 37500-903
Itajubá, MG, Brasil
email: jacson@unifei.edu.br
|
|---|
 |
Mariza Stefanello Simsen
Instituto de Matemática e Computação
Universidade Federal de Itajubá, Av. BPS n.1303,
Bairro Pinheirinho, 37500-903
Itajubá, MG, Brasil
email: mariza@unifei.edu.br
|
|---|
Return to the EJDE web page

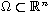 ,
,
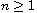 ,
is a bounded
domain with Lipschitz-continuous boundary. The exponent p(x) is
a given measurable function,
,
is a bounded
domain with Lipschitz-continuous boundary. The exponent p(x) is
a given measurable function,
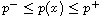 a.e. in
a.e. in
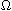 for some bounded constants
for some bounded constants
 and
and
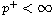 .
It is assumed that
.
It is assumed that
 ,
and that the multivalued function
,
and that the multivalued function
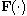 is globally Lipschitz, has convex closed values and
is globally Lipschitz, has convex closed values and
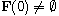 . We prove that the homogeneous
Dirichlet problem has a local in time weak solution. Also we show that
when
. We prove that the homogeneous
Dirichlet problem has a local in time weak solution. Also we show that
when
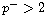 and
and
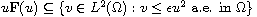 with a sufficiently small
with a sufficiently small
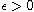 the weak solution possesses
the property of finite speed of propagation of disturbances from
the initial data and may exhibit the waiting time property.
Estimates on the evolution of the null-set of the solution are
presented.
the weak solution possesses
the property of finite speed of propagation of disturbances from
the initial data and may exhibit the waiting time property.
Estimates on the evolution of the null-set of the solution are
presented.



