In this article we study discrete nonlinear Schrodinger equations without periodicity assumptions. We show the existence of multiple solutions of the form
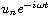(called breathers)
by using Clark's Theorem in critical point theory.
Tao Zhou, Xia Liu, Haiping Shi, Zongliang Wen
Abstract:
In this article we study discrete nonlinear Schrodinger equations
without periodicity assumptions. We show the existence of
multiple solutions of the form
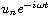(called breathers)
by using Clark's Theorem in critical point theory.
Submitted March 28, 2018. Published February 14, 2019.
Math Subject Classifications: 39A12, 39A70, 35C08.
Key Words: Breather; discrete nonlinear Schrodinger equation; subquadratic;
critical point.
Show me the PDF file (245 KB), TEX file for this article.
 |
Tao Zhou School of Public Administration and Emergency Management Jinan University Guangzhou 510632, China email: zhoutaoscut@hotmail.com |
|---|---|
 |
Xia Liu College of Continuing Education and Open College Guangdong University of Foreign Studies Guangzhou 510420, China email: xia991002@163.com |
 |
Haiping Shi Modern Business and Management Department Guangdong Construction Polytechnic Guangzhou 510440, China email: shp7971@163.com |
 |
Zongliang Wen College of Pharmacy Guangxi University of Chinese Medicine Nanning 530001, China email: mathwzl@163.com |
Return to the EJDE web page