Electron. J. Differential Equations,
Vol. 2019 (2019), No. 28, pp. 1-23.
Ground state, bound states and bifurcation properties for a
Schrodinger-Poisson system with critical exponent
Jianqing Chen, Lirong Huang, Eugenio M. Rocha
Abstract:
This article concerns the existence of ground state and bound states,
and the study of their bifurcation properties for the Schrodinger-Poisson
system
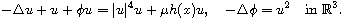
Under suitable assumptions on the coefficient h(x), we prove that
the ground state must bifurcate from zero, and that another bound state
bifurcates from a solution, when
 is the first eigenvalue of
is the first eigenvalue of
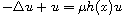 in
in
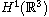 .
.
Submitted April 22, 2018. Published February 18, 2019.
Math Subject Classifications: 35J20, 35J70.
Key Words: Ground state and bound states; bifurcation properties;
Schrodinger-Poisson system; variational method.
Show me the PDF file (334 KB),
TEX file for this article.
 |
Jianqing Chen
College of Mathematics and Informatics & FJKLMAA
Fujian Normal University
Qishan Campus, Fuzhou 350108, China
email: jqchen@fjnu.edu.cn
|
|---|
 |
Lirong Huang
College of Mathematics and Physics
Fujian Jiangxia University
Fuzhou 350108, China
email: lrhuang515@126.com
|
|---|
 |
Eugénio M. Rocha
Department of Mathematics
University of Aveiro, 3810-193
Aveiro, Portugal
email: eugenio@ua.pt
|
|---|
Return to the EJDE web page
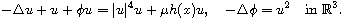
 is the first eigenvalue of
is the first eigenvalue of
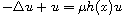 in
in
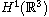 .
.


