Electron. J. Differential Equations, Vol. 2019 (2019), No. 30, pp. 1-11.

Stability of nonlinear Volterra integro-differential equations with Caputo fractional derivative and bounded delays

Snezhana Hristova, Cemil Tunc

Abstract:
We use Lyapunov functions to study stability of the first-order Volterra integro-differential equation with Caputo fractional derivative
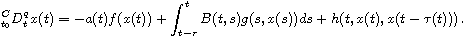
$$ {}_{t_0}^{C}D^{q}_tx(t) =-a(t)f(x(t)) +\int_{t-r}^tB(t,s)g(s,x(s))ds+h(t,x(t),x(t-\tau(t))) \,. $$
For the Lyapunov functions, we consider three types of fractional derivatives. By means of these derivatives, we obtain new sufficient conditions for stability and uniformly stability of solutions We consider both constant and time variable bounded delays, and illustrated our results with an example.

Submitted January 6, 2019. Published February 19, 2019.
Math Subject Classifications: 26A33, 34A08, 34D20, 34K20.
Key Words: Fractional derivative; integro-differential equation; delay; Lyapunov functional; stability.

Show me the PDF file (391 KB), TEX file for this article.

Snezhana Hristova
Department of Applied Mathematics and Modeling
University of Plovdiv "Paisii Hilendarski"
4000 Plovdiv, Bulgaria
email: snehri@gmail.com
Cemil Tunc
Department of Mathematics, Faculty of Sciences
Van Yuzuncu Yil University
65080 Van, Turkey
email: cemtunc@yahoo.com

Return to the EJDE web page