Electron. J. Differential Equations,
Vol. 2019 (2019), No. 32, pp. 1-29.
Bifurcation from the first eigenvalue of the p-Laplacian with
nonlinear boundary condition
Mabel Cuesta, Liamidi A. Leadi, Pascaline Nshimirimana
Abstract:
We consider the problem
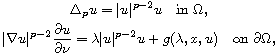
where
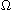 is a bounded domain of
is a bounded domain of
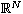 with smooth boundary,
with smooth boundary,
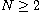 ,
and
,
and
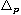 denotes the p-Laplacian operator. We
give sufficient conditions for the existence of continua of solutions
bifurcating from both zero and infinity at the principal eigenvalue
of p-Laplacian with nonlinear boundary conditions.
We also prove that those continua split on two, one containing strictly positive
and the other containing strictly negative solutions. As an application
we deduce results on anti-maximum and maximum principles for the
p-Laplacian operator with nonlinear boundary conditions.
denotes the p-Laplacian operator. We
give sufficient conditions for the existence of continua of solutions
bifurcating from both zero and infinity at the principal eigenvalue
of p-Laplacian with nonlinear boundary conditions.
We also prove that those continua split on two, one containing strictly positive
and the other containing strictly negative solutions. As an application
we deduce results on anti-maximum and maximum principles for the
p-Laplacian operator with nonlinear boundary conditions.
Submitted July 19, 2018. Published February 21, 2019.
Math Subject Classifications: 35J92, 35J65, 35J60, 35B32, 35B50.
Key Words: Bifurcation theory; topological degree;
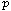 -Laplacian;
elliptic problem; nonlinear boundary condition;
maximum and anti-maximum principles.
-Laplacian;
elliptic problem; nonlinear boundary condition;
maximum and anti-maximum principles.
Show me the PDF file (400 KB),
TEX file for this article.
 |
Mabel Cuesta
Laboratoire de Mathématiques Pures et Appliquées
Université du Littoral Côte d'Opale (ULCO)
50, rue F. Buisson, BP: 699
62228 Calais, France
email: cuesta-l@univ-littoral.fr
|
|---|
 |
Liamidi Leadi
Département de Mathématiques, Faculté
des Sciences et Techniques
Institut de Mathématiques et de Sciences Physiques (IMSP)
Université d'Abomey-Calavi (UAC)
01 BP 613, Porto-Novo, Benin
email: leadiare@imsp-uac.org, leadiare@yahoo.com
|
|---|
 |
Pascaline Nshimirimana
Institut de Mathématiques et de Sciences Physiques (IMSP)
Université d'Abomey-Calavi (UAC)
01 BP 613, Porto-Novo, Benin
email: pascaline.nshimirimana@imsp-uac.org,
nshimirimanapascaline@yahoo.fr
|
|---|
Return to the EJDE web page
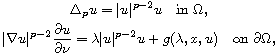
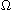 is a bounded domain of
is a bounded domain of
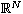 with smooth boundary,
with smooth boundary,
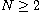 ,
and
,
and
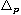 denotes the p-Laplacian operator. We
give sufficient conditions for the existence of continua of solutions
bifurcating from both zero and infinity at the principal eigenvalue
of p-Laplacian with nonlinear boundary conditions.
We also prove that those continua split on two, one containing strictly positive
and the other containing strictly negative solutions. As an application
we deduce results on anti-maximum and maximum principles for the
p-Laplacian operator with nonlinear boundary conditions.
denotes the p-Laplacian operator. We
give sufficient conditions for the existence of continua of solutions
bifurcating from both zero and infinity at the principal eigenvalue
of p-Laplacian with nonlinear boundary conditions.
We also prove that those continua split on two, one containing strictly positive
and the other containing strictly negative solutions. As an application
we deduce results on anti-maximum and maximum principles for the
p-Laplacian operator with nonlinear boundary conditions.
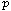 -Laplacian;
elliptic problem; nonlinear boundary condition;
maximum and anti-maximum principles.
-Laplacian;
elliptic problem; nonlinear boundary condition;
maximum and anti-maximum principles.


