We investigate the existence of solutions in modular function spaces of the Fredholm integral equation
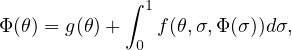
where
![$\Phi(\theta), g(\theta)\in L_{\rho}, \theta\in [0,1],
f: [0,1]\times[0,1]\times L_{\rho}\to \mathbb{R}$](images/formula1x.png)
.
An application in the variable exponent Lebesgue spaces is
derived under minimal assumptions on the problem data.
Mostafa Bachar
Abstract:
We investigate the existence of solutions in modular function spaces
of the Fredholm integral equation
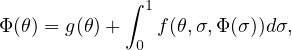
where
.
An application in the variable exponent Lebesgue spaces is
derived under minimal assumptions on the problem data.
Submitted March 13, 2018. Published March 5, 2019.
Math Subject Classifications: 46A80, 47H10, 45G05.
Key Words: Electrorheological fluids; fixed point; Fredholm equations;
modular function spaces; variable exponent spaces.
Show me the PDF file (322 KB), TEX file for this article.
 |
Mostafa Bachar College of Sciences Department of Mathematics King Saud University Riyadh, Saudi Arabia email: mbachar@ksu.edu.sa |
|---|
Return to the EJDE web page