Electron. J. Differential Equations,
Vol. 2019 (2019), No. 38, pp. 1-19.
Renormalized solutions to a chemotaxis system with consumption of chemoattractant
Hengling Wang, Yuxiang Li
Abstract:
This article concerns the high-dimensional chemotaxis system with consumption
of chemoattractant
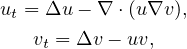
under homogeneous boundary conditions of Neumann type, in a bounded domain
 with smooth boundary. We prove that that if
the initial data satisfy
with smooth boundary. We prove that that if
the initial data satisfy
 and
and
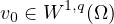 for some
for some
 ,
this model possesses at least one global renormalized solution.
,
this model possesses at least one global renormalized solution.
Submitted May 19, 2018. Published March 11, 2019.
Math Subject Classifications: 35A01, 35K57, 35Q92, 92C17
Key Words: Keller-Segel model; renormalized solutions; entropy method
Show me the PDF file (385 KB),
TEX file for this article.
 |
Hengling Wang
Institute for Applied Mathematics
School of Mathematics, Southeast University
Nanjing 211189, China
email: hlwang@seu.edu.cn
|
|---|
 |
Yuxiang Li
Institute for Applied Mathematics
School of Mathematics
Southeast University
Nanjing 211189, China
email: lieyx@seu.edu.cn
|
|---|
Return to the EJDE web page
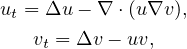
 with smooth boundary. We prove that that if
the initial data satisfy
with smooth boundary. We prove that that if
the initial data satisfy
 and
and
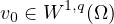 for some
for some
 ,
this model possesses at least one global renormalized solution.
,
this model possesses at least one global renormalized solution.

