In this article, we study a class of generalized extensible beam equations with a superlinear nonlinearity
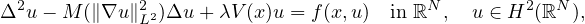
where
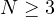 ,
,
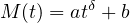 with
with
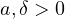 and
and
 ,
,
 is a parameter,
is a parameter,
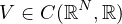 and
and
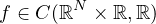 .
Unlike most other papers on this problem, we allow the constant
.
Unlike most other papers on this problem, we allow the constant
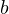 to be
non-positive, which has the physical significance. Under some suitable
assumptions on
to be
non-positive, which has the physical significance. Under some suitable
assumptions on
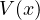 and
and
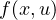 , when
, when
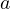 is small and
is small and
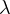 is
large enough, we prove the existence of two nontrivial solutions
is
large enough, we prove the existence of two nontrivial solutions
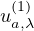 and
and
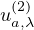 ,
one of which will blow up as the nonlocal term vanishes. Moreover,
,
one of which will blow up as the nonlocal term vanishes. Moreover,
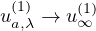 and
and
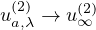 strongly in
strongly in
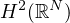 as
as
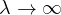 ,
where
,
where
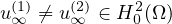 are two
nontrivial solutions of Dirichlet BVPs on the bounded domain
are two
nontrivial solutions of Dirichlet BVPs on the bounded domain
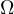 .
Also, the nonexistence of nontrivial solutions is also obtained for
.
Also, the nonexistence of nontrivial solutions is also obtained for
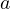 large enough.
large enough.

