Electron. J. Differential Equations,
Vol. 2019 (2019), No. 43, pp. 1-17.
Fast homoclinic solutions for damped vibration systems
with subquadratic and asymptotically quadratic potentials
Yiwei Ye
Abstract:
In this article, we study the nonperiodic damped vibration problem
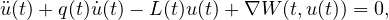
where L(t) is uniformly positive definite for all
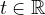 ,
and W(t,x) is either subquadratic or asymptotically
quadratic in x as
,
and W(t,x) is either subquadratic or asymptotically
quadratic in x as
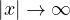 .
Based on the minimax
method in critical point theory, we prove the existence and
multiplicity of fast homoclinic solutions for the above problem.
.
Based on the minimax
method in critical point theory, we prove the existence and
multiplicity of fast homoclinic solutions for the above problem.
Submitted November 3, 2017. Published March 22, 2019.
Math Subject Classifications: 34C37, 37J45.
Key Words: Fast homoclinic solutions; damped vibration problem;
subquadratic; asymptotically quadratic.
Show me the PDF file (360 KB),
TEX file for this article.
 |
Yiwei Ye
School of Mathematical Science
Chongqing Normal University
Chongqing 401331, China
email: yeyiwei2011@126.com
|
|---|
Return to the EJDE web page
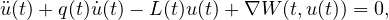
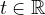 ,
and W(t,x) is either subquadratic or asymptotically
quadratic in x as
,
and W(t,x) is either subquadratic or asymptotically
quadratic in x as
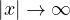 .
Based on the minimax
method in critical point theory, we prove the existence and
multiplicity of fast homoclinic solutions for the above problem.
.
Based on the minimax
method in critical point theory, we prove the existence and
multiplicity of fast homoclinic solutions for the above problem.
