Electron. J. Differential Equations,
Vol. 2019 (2019), No. 48, pp. 1-22.
Compactness of the canonical solution operator on
Lipschitz q-pseudoconvex boundaries
Sayed Saber
Abstract:
Let
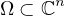 be a bounded Lipschitz q-pseudoconvex
domain that admit good weight functions. We shall prove that the canonical
solution operator for the
be a bounded Lipschitz q-pseudoconvex
domain that admit good weight functions. We shall prove that the canonical
solution operator for the
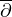 -equation is compact on
the boundary of
-equation is compact on
the boundary of
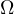 and is bounded in the Sobolev space
and is bounded in the Sobolev space
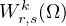 for some values of k. Moreover, we show that
the Bergman projection and the
for some values of k. Moreover, we show that
the Bergman projection and the
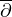 -Neumann operator
are bounded in the Sobolev space
-Neumann operator
are bounded in the Sobolev space
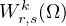 for some values of k.
If
for some values of k.
If
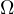 is smooth, we shall give sufficient conditions for compactness
of the
is smooth, we shall give sufficient conditions for compactness
of the
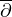 -Neumann operator.
-Neumann operator.
Submitted May 8, 2018. Published April 10, 2019.
Math Subject Classifications: 35J20, 35J25, 35J60.
Key Words: Lipschitz domain; q-pseudoconvex domain.
Show me the PDF file (407 KB),
TEX file for this article.
 |
Sayed Saber
Faculty of Science and Arts in Baljurashi
Albaha University
Albaha, Saudi Arabia
email: sayedkay@yahoo.com
|
|---|
Return to the EJDE web page
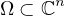 be a bounded Lipschitz q-pseudoconvex
domain that admit good weight functions. We shall prove that the canonical
solution operator for the
be a bounded Lipschitz q-pseudoconvex
domain that admit good weight functions. We shall prove that the canonical
solution operator for the
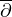 -equation is compact on
the boundary of
-equation is compact on
the boundary of
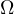 and is bounded in the Sobolev space
and is bounded in the Sobolev space
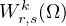 for some values of k. Moreover, we show that
the Bergman projection and the
for some values of k. Moreover, we show that
the Bergman projection and the
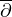 -Neumann operator
are bounded in the Sobolev space
-Neumann operator
are bounded in the Sobolev space
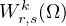 for some values of k.
If
for some values of k.
If
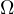 is smooth, we shall give sufficient conditions for compactness
of the
is smooth, we shall give sufficient conditions for compactness
of the
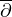 -Neumann operator.
-Neumann operator.
