Electron. J. Differential Equations,
Vol. 2019 (2019), No. 49, pp. 1-32.
Regularity of the lower positive branch for singular elliptic bifurcation problems
Tomas Godoy, Alfredo Guerin
Abstract:
We consider the problem
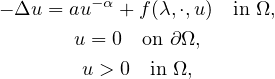
where
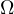 is a bounded domain in
is a bounded domain in
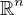 ,
,
 ,
,
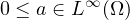 , and
, and
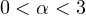 .
It is known that, under suitable assumptions on f, there exists
.
It is known that, under suitable assumptions on f, there exists
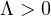 such that this problem has at least one weak solution in
such that this problem has at least one weak solution in
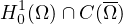 if and only if
if and only if
![$\lambda\in[0,\Lambda] $](images/a8x.png) ;
and that, for
;
and that, for
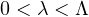 ,
at least two such solutions exist. Under additional hypothesis on a
and f, we prove regularity properties of the branch formed by the minimal
weak solutions of the above problem. As a byproduct of the method used,
we obtain the uniqueness of the positive solution when
,
at least two such solutions exist. Under additional hypothesis on a
and f, we prove regularity properties of the branch formed by the minimal
weak solutions of the above problem. As a byproduct of the method used,
we obtain the uniqueness of the positive solution when
 .
.
Submitted August 7, 2018. Published April 12, 2019.
Math Subject Classifications: 35J75, 35D30, 35J20.
Key Words: Singular elliptic problems; positive solutions; bifurcation problems;
implicit function theorem; sub and super solutions.
Show me the PDF file (494 KB),
TEX file for this article.
 |
Tomas Godoy
FaMAF, Universidad Nacional de Córdoba
(5000) Córdoba, Argentina
email: godoy@mate.uncor.edu
|
|---|
| |
Alfredo Guerin
FaMAF, Universidad Nacional de Córdoba
(5000) Córdoba, Argentina
email: guerin.alfredojose@gmail.com
|
|---|
Return to the EJDE web page
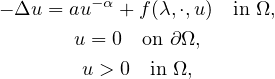
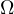 is a bounded domain in
is a bounded domain in
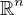 ,
,
 ,
,
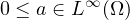 , and
, and
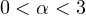 .
It is known that, under suitable assumptions on f, there exists
.
It is known that, under suitable assumptions on f, there exists
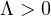 such that this problem has at least one weak solution in
such that this problem has at least one weak solution in
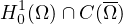 if and only if
if and only if
![$\lambda\in[0,\Lambda] $](images/a8x.png) ;
and that, for
;
and that, for
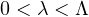 ,
at least two such solutions exist. Under additional hypothesis on a
and f, we prove regularity properties of the branch formed by the minimal
weak solutions of the above problem. As a byproduct of the method used,
we obtain the uniqueness of the positive solution when
,
at least two such solutions exist. Under additional hypothesis on a
and f, we prove regularity properties of the branch formed by the minimal
weak solutions of the above problem. As a byproduct of the method used,
we obtain the uniqueness of the positive solution when
 .
.
