We consider a family of linear singularly perturbed Cauchy problems which combines partial differential operators and linear fractional transforms. This work is the sequel of a study initiated in [17]. We construct a collection of holomorphic solutions on a full covering by sectors of a neighborhood of the origin in
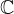 with respect to
the perturbation parameter
with respect to
the perturbation parameter
 . This set is built up through
classical and special Laplace transforms along piecewise linear paths of
functions which possess exponential or super exponential growth/decay on
horizontal strips.
A fine structure which entails two levels of Gevrey asymptotics of order
1 and so-called order
. This set is built up through
classical and special Laplace transforms along piecewise linear paths of
functions which possess exponential or super exponential growth/decay on
horizontal strips.
A fine structure which entails two levels of Gevrey asymptotics of order
1 and so-called order
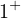 is presented. Furthermore, unicity properties
regarding the
is presented. Furthermore, unicity properties
regarding the
 asymptotic layer are observed and follow from results
on summability with respect to a particular strongly regular sequence
recently obtained in [13].
asymptotic layer are observed and follow from results
on summability with respect to a particular strongly regular sequence
recently obtained in [13].

