Electron. J. Differential Equations,
Vol. 2019 (2019), No. 61, pp. 1-18.
Decay rate of strong solutions to compressible Navier-Stokes-Poisson equations
with external force
Yeping Li, Nengqiu Zhang
Abstract:
In this article, we consider the three dimensional compressible
Navier-Stokes-Poisson equations with the effect of external
potential force. First, the stationary solution is established by
solving a nonlinear elliptic system. Next, we show global well-posedness
of the strong solutions for the initial value problem to the three
dimensional compressible Navier-Stokes-Poisson equations when the
initial data are close to the stationary solution in
 .
Moreover, if the
.
Moreover, if the
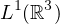 -norm of initial perturbation is finite,
we prove the optimal
-norm of initial perturbation is finite,
we prove the optimal
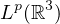
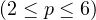 decay rates for such
strong solution and
decay rates for such
strong solution and
 decay rate of its first-order
spatial derivatives via a low frequency and high frequency decomposition.
decay rate of its first-order
spatial derivatives via a low frequency and high frequency decomposition.
Submitted October 7, 2018. Published May 7, 2019.
Math Subject Classifications: 35M20, 35Q35, 76W05.
Key Words: Navier-Stokes-Poisson equation; stationary solution;
strong solution; energy estimate; optimal decay rate.
Show me the PDF file (365 KB),
TEX file for this article.
 |
Yeping Li
Department of Mathematics
East China University of Science and Technology
Shanghai 200237, China
email: yplee@ecust.edu.cn
|
|---|
| |
Nengqiu Zhang
Department of Mathematics
East China University of Science and Technology
Shanghai 200237, China
email: 731835397@qq.com
|
|---|
Return to the EJDE web page
 .
Moreover, if the
.
Moreover, if the
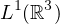 -norm of initial perturbation is finite,
we prove the optimal
-norm of initial perturbation is finite,
we prove the optimal
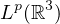
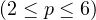 decay rates for such
strong solution and
decay rates for such
strong solution and
 decay rate of its first-order
spatial derivatives via a low frequency and high frequency decomposition.
decay rate of its first-order
spatial derivatives via a low frequency and high frequency decomposition.
