We study the nonlinear eigenvalue problem
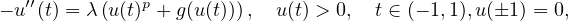
where
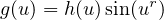 ,
,
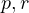 are given constants
satisfying
are given constants
satisfying
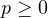 ,
,
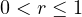 and
and
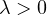 is a parameter.
It is known that under suitable conditions on
is a parameter.
It is known that under suitable conditions on
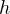 ,
,
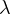 is
parameterized by the maximum norm
is
parameterized by the maximum norm
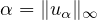 of the solution
of the solution
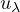 associated with
associated with
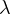 and
and
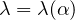 is a continuous
function for
is a continuous
function for
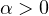 .
When
.
When
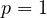 ,
,
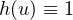 and
and
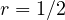 ,
this equation has been introduced
by Chen [4] as a model equation such that there exist infinitely many solutions
near
,
this equation has been introduced
by Chen [4] as a model equation such that there exist infinitely many solutions
near
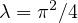 .
We prove that
.
We prove that
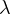 is an oscillatory bifurcation curve as
is an oscillatory bifurcation curve as
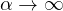 by showing the asymptotic formula for
by showing the asymptotic formula for
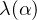 .
It is found that the shapes of bifurcation curves
depend on the condition
.
It is found that the shapes of bifurcation curves
depend on the condition
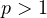 or
or
 .
time-map argument and stationary phase method.
.
time-map argument and stationary phase method.
