We characterize the centers of the Chiellini Hamiltonian Lienard second-order differential equations
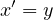 ,
,
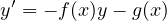 where
where
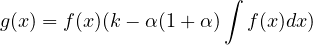 with
with
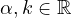 . Moreover we study the phase portraits
in the Poincare disk of these systems when
. Moreover we study the phase portraits
in the Poincare disk of these systems when
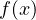 is linear.
is linear.
Jaume Gine, Jaume Llibre, Claudia Valls
Abstract:
We characterize the centers of the Chiellini Hamiltonian Lienard
second-order differential equations
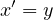 ,
,
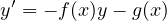 where
where
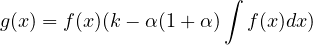 with
with
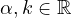 . Moreover we study the phase portraits
in the Poincare disk of these systems when
. Moreover we study the phase portraits
in the Poincare disk of these systems when
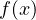 is linear.
is linear.
Submitted January 26, 2019. Published May 17, 2019.
Math Subject Classifications: 34C05, 34A34, 34C14.
Key Words: Lienard system; center-focus problem; first integrals.
Show me the PDF file (407 KB), TEX file for this article.
 |
Jaume Giné Departament de Matemàtica Inspires Research Centre Universitat de Lleida Avda. Jaume II, 69 25001 Lleida, Catalonia, Spain email: gine@matematica.udl.cat |
|---|---|
 |
Jaume Llibre Departament de Matemàtiques Universitat Autònoma de Barcelona 08193 Bellaterra, Barcelona, Catalonia, Spain email: jllibre@mat.uab.cat |
| Claudia Valls Departamento de Matemática Instituto Superior Técnico Av. Rovisco Pais 1049-001 Lisboa, Portugal email: cvalls@math.ist.utl.pt |
Return to the EJDE web page