Electron. J. Differential Equations, Vol. 2019 (2019), No. 73, pp. 1-12.

Travelling solitary waves for boson stars

Guoqing Zhang, Ningning Song

Abstract:
In this article, we study the pseudo-relativistic Hartree equation
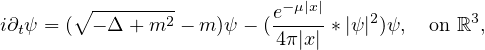
$$ i\partial_{t}\psi=(\sqrt{-\Delta+m^2}-m)\psi -(\frac{e^{-\mu|x|}}{4\pi|x|}\ast|\psi|^2)\psi,\quad \text{on }\mathbb{R}^3, $$
which describes the dynamics of pseudo-relativistic boson stars with rest mass m>0 in the mean-field limit. Based on Ekeland variational principle, concentration-compactness lemma and Gagliardo-Nirenberg inequality, we prove existence of travelling solitary waves under the critical stellar mass. In addition to their existence, we obtain orbital stability by using a general idea presented in Cazenave and Lions [2].

Submitted July 3, 2018. Published May 28, 2019.
Math Subject Classifications: 35Q40, 35Q55, 47J35.
Key Words: Travelling solitary wave; boson star equation; critical stellar mass.

Show me the PDF file (355 KB), TEX file for this article.

Guoqing Zhang
College of Sciences
University of Shanghai for Science and Technology
Shanghai 200093, China
email: shzhangguoqing@126.com
Ningning Song
College of Sciences
University of Shanghai for Science and Technology
Shanghai 200093, China
email: 787661389@qq.com

Return to the EJDE web page