Electron. J. Differential Equations,
Vol. 2019 (2019), No. 76, pp. 1-17.
Crank-Nicolson Legendre spectral approximation for space-fractional
Allen-Cahn equation
Wenping Chen, Shujuan Lu, Hu Chen, Haiyu Liu
Abstract:
In this article, we consider spectral methods for solving the
initial-boundary value problem of the space fractional-order
Allen-Cahn equation.
A fully discrete scheme based on the modified Crank-Nicolson scheme in
time and the Legendre spectral method in space is established.
The existence and uniqueness of the fully discrete scheme are derived,
and the stability and convergence analysis of the fully discrete scheme
are proved rigorously.
By constructing a fractional duality argument, the corresponding optimal
error estimates in
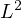 and
and
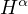 norm are derived, respectively.
Also, numerical experiments are performed to support the theoretical results.
norm are derived, respectively.
Also, numerical experiments are performed to support the theoretical results.
Submitted August 28, 2018. Published May 31, 2019.
Math Subject Classifications: 35R11, 65M06, 65M70, 65M12.
Key Words: Space-fractional Allen-Cahn equation; Legendre spectral method;
modified Crank-Nicolson scheme; stability; convergence.
Show me the PDF file (374 KB),
TEX file for this article.
 |
Wenping Chen
School of Mathematics and Systems Science & LMIB
Beijing University of Aeronautics & Astronautics
Beijing, 100191, China
email: anhuicwp@163.com
|
|---|
| |
Shujuan Lu
School of Mathematics and Systems Science & LMIB
Beijing University of Aeronautics & Astronautics
Beijing, 100191, China
email: lsj@buaa.edu.cn
|
|---|
 |
Hu Chen
Beijing Computational Science Research Center
Beijing, 100193, China
email: chenhuwenlong@126.com
|
|---|
 |
Haiyu Liu
School of Mathematics and Systems Science & LMIB
Beijing University of Aeronautics & Astronautics
Beijing, 100191, China
email: liuhaiyu0415@163.com
|
|---|
Return to the EJDE web page
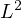 and
and
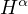 norm are derived, respectively.
Also, numerical experiments are performed to support the theoretical results.
norm are derived, respectively.
Also, numerical experiments are performed to support the theoretical results.


