Electron. J. Differential Equations,
Vol. 2019 (2019), No. 87, pp. 1-20.
Existence of infinitely many solutions of p-Laplacian equations in R^N+
Junfang Zhao, Xiangqing Liu, Jiaquan Liu
Abstract:
In this article, we study the p-Laplacian equation
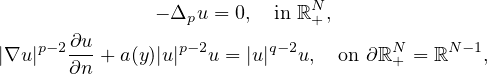
where
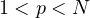 ,
,
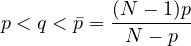 ,
,
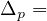 div
div
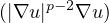 the p-Laplacian operator,
and the positive, finite function a(y) satisfies suitable decay
assumptions at infinity. By using the truncation method, we prove the
existence of infinitely many solutions.
the p-Laplacian operator,
and the positive, finite function a(y) satisfies suitable decay
assumptions at infinity. By using the truncation method, we prove the
existence of infinitely many solutions.
Submitted September 22, 2018. Published July 16, 2019.
Math Subject Classifications: 35B05, 35B45.
Key Words: p-Lalacian equation; half space; boundary value problem;
multiple solutions; truncation method.
Show me the PDF file (411 KB),
TEX file for this article.
 |
Junfang Zhao
School of Science
China University of Geosciences
Beijing 100083, China
email: zhao_junfang@163.com
|
|---|
| |
Xiangqing Liu
Department of Mathematics
Yunnan Normal University
Kunming 650500, China
email: lxq8u8@163.com
|
|---|
| |
Jiaquan Liu
LMAM, School of Mathematics
Peking University
Beijing 100871, China
email: jiaquan@math.pku.edu.cn
|
|---|
Return to the EJDE web page
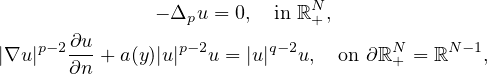
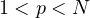 ,
,
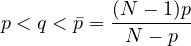 ,
,
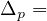 div
div
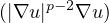 the p-Laplacian operator,
and the positive, finite function a(y) satisfies suitable decay
assumptions at infinity. By using the truncation method, we prove the
existence of infinitely many solutions.
the p-Laplacian operator,
and the positive, finite function a(y) satisfies suitable decay
assumptions at infinity. By using the truncation method, we prove the
existence of infinitely many solutions.
