Electron. J. Differential Equations,
Vol. 2019 (2019), No. 90, pp. 1-32.
Existence of solutions for non-local elliptic systems with
Hardy-Littlewood-Sobolev critical nonlinearities
Yang Yang, Qian Yu Hong, Xudong Shang
Abstract:
In this work, we establish the existence of solutions for the nonlinear
nonlocal system of equations involving the fractional Laplacian,
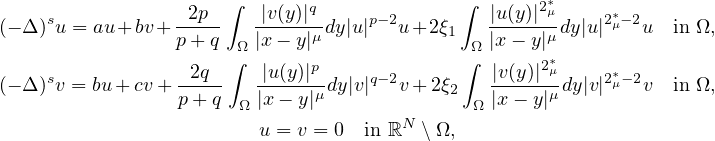
where
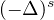 is the fractional Laplacian operator,
is the fractional Laplacian operator,
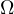 is a smooth bounded domain in
is a smooth bounded domain in
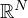 ,
,
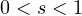 ,
,
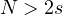 ,
,
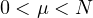 ,
,
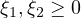 ,
,
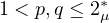 and
and
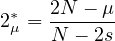 is the upper critical exponent in
the Hardy-Littlewood-Sobolev inequality.
The nonlinearities can interact with the spectrum of the fractional Laplacian.
More specifically, the interval defined by the two eigenvalues of the real
matrix from the linear part contains an eigenvalue of the spectrum of
the fractional Laplacian. In this case, resonance phenomena can occur.
is the upper critical exponent in
the Hardy-Littlewood-Sobolev inequality.
The nonlinearities can interact with the spectrum of the fractional Laplacian.
More specifically, the interval defined by the two eigenvalues of the real
matrix from the linear part contains an eigenvalue of the spectrum of
the fractional Laplacian. In this case, resonance phenomena can occur.
Submitted December 11, 2018. Published July 19, 2019.
Math Subject Classifications: 35R11, 35R09, 35A15.
Key Words: Fractional Laplacian; Choquard equation; Linking theorem;
Hardy-Littlewood-Sobolev critical exponent; Mountain Pass theorem.
Show me the PDF file (482 KB),
TEX file for this article.
 |
Yang Yang
School of Science
Jiangnan University
Wuxi, Jiangsu 214122, China
email: yynjnu@126.com
|
|---|
 |
Qian Yu Hong
School of Science
Jiangnan University
Wuxi, Jiangsu 214122, China
email: 1031369190@qq.com
|
|---|
 |
Xudong Shang
School of Mathematics
Nanjing Normal University, Taizhou College
Taizgou, Jiangsu 225300, China
email: xudong-shang@163.com
|
|---|
Return to the EJDE web page
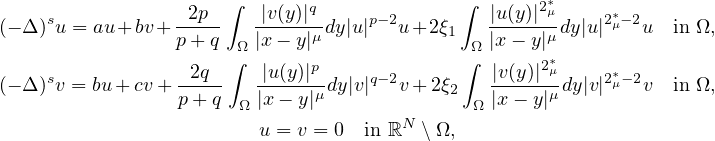
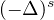 is the fractional Laplacian operator,
is the fractional Laplacian operator,
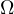 is a smooth bounded domain in
is a smooth bounded domain in
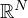 ,
,
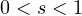 ,
,
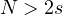 ,
,
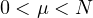 ,
,
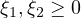 ,
,
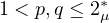 and
and
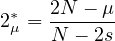 is the upper critical exponent in
the Hardy-Littlewood-Sobolev inequality.
The nonlinearities can interact with the spectrum of the fractional Laplacian.
More specifically, the interval defined by the two eigenvalues of the real
matrix from the linear part contains an eigenvalue of the spectrum of
the fractional Laplacian. In this case, resonance phenomena can occur.
is the upper critical exponent in
the Hardy-Littlewood-Sobolev inequality.
The nonlinearities can interact with the spectrum of the fractional Laplacian.
More specifically, the interval defined by the two eigenvalues of the real
matrix from the linear part contains an eigenvalue of the spectrum of
the fractional Laplacian. In this case, resonance phenomena can occur.


