We study the long-time behavior of solutions to a particular class of nonlinear wave equations that appear in models for waves traveling in a non-homogeneous gas with variable damping. Specifically, decay estimates for the energy of such solutions are established. We find three different regimes of energy decay depending on the exponent of the absorption term
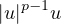 and show the existence of two
critical exponents
and show the existence of two
critical exponents
 and
and
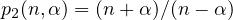 .
For
.
For
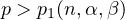 ,
the decay of solutions of the nonlinear equation
coincides with that of the corresponding linear problem.
For
,
the decay of solutions of the nonlinear equation
coincides with that of the corresponding linear problem.
For
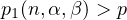 ,
the solution decays much faster. The other
critical exponent
,
the solution decays much faster. The other
critical exponent
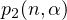 further divides this region
into two subregions with different decay rates. Deriving the sharp decay of
solutions even for the linear problem with potential
further divides this region
into two subregions with different decay rates. Deriving the sharp decay of
solutions even for the linear problem with potential
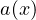 is a delicate
task and requires serious strengthening of the multiplier method. Here we use
a modification of an approach of Todorova and Yordanov to derive the exact
decay of the nonlinear equation.
is a delicate
task and requires serious strengthening of the multiplier method. Here we use
a modification of an approach of Todorova and Yordanov to derive the exact
decay of the nonlinear equation.
