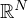
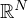
Bryan P. Rynne
Abstract:
We consider the parabolic initial-boundary value problem

where
 is the unit ball centered at the origin in
is the unit ball centered at the origin in
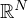 ,
with
,
with
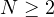 ,
,
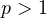 , and
, and
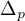 denotes the p-Laplacian on
denotes the p-Laplacian on
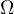 .
The function
.
The function
![$f:[0,1]\times{\mathbb R}\to{\mathbb R}$](images/a7x.png) is continuous, and the
partial derivative
is continuous, and the
partial derivative
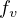 exists and is continuous and bounded on
exists and is continuous and bounded on
![$[0,1]\times{\mathbb R}$](images/a9x.png) .
It will be shown that (under certain additional hypotheses) the
"principle of linearized stability" holds for radially symmetric equilibrium
solutions
.
It will be shown that (under certain additional hypotheses) the
"principle of linearized stability" holds for radially symmetric equilibrium
solutions
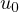 of the equation.
That is, the asymptotic stability, or instability, of
of the equation.
That is, the asymptotic stability, or instability, of
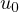 is determined by
the sign of the principal eigenvalue of a linearization of the problem at
is determined by
the sign of the principal eigenvalue of a linearization of the problem at
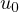 .
It is well-known that this principle holds for the semilinear case p=2
(
.
It is well-known that this principle holds for the semilinear case p=2
(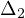 is the linear Laplacian), but has not been shown to hold when
is the linear Laplacian), but has not been shown to hold when
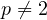 .
We also consider a bifurcation type problem similar to the one above, having a
line of trivial solutions and a curve of non-trivial solutions bifurcating
from the line of trivial solutions at the principal eigenvalue of the p-Laplacian.
We characterize the stability, or instability, of both the trivial solutions and
the non-trivial bifurcating solutions, in a neighbourhood of the bifurcation point,
and we obtain a result on "exchange of stability" at the bifurcation point,
analogous to the well-known result when p=2.
.
We also consider a bifurcation type problem similar to the one above, having a
line of trivial solutions and a curve of non-trivial solutions bifurcating
from the line of trivial solutions at the principal eigenvalue of the p-Laplacian.
We characterize the stability, or instability, of both the trivial solutions and
the non-trivial bifurcating solutions, in a neighbourhood of the bifurcation point,
and we obtain a result on "exchange of stability" at the bifurcation point,
analogous to the well-known result when p=2.
Submitted November 27, 2018. Published July 29, 2019.
Math Subject Classifications: 35B35, 35B32, 35K55.
Key Words: p-Laplacian; parabolic boundary value problem; stability; bifurcation.
Show me the PDF file (384 KB), TEX file for this article.
 |
Bryan P. Rynne Department of Mathematics and the Maxwell Institute for Mathematical Sciences Heriot-Watt University Edinburgh EH14 4AS, Scotland, UK email: B.P.Rynne@hw.ac.uk |
|---|
Return to the EJDE web page