In this article we present some nonexistence results concerning stable solutions to the equation
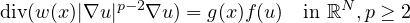
when f(u) is either
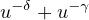 with
with
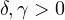 or
or
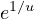 where w,g are suitable weight functions.
where w,g are suitable weight functions.
Kaushik Bal, Prashanta Garain
Abstract:
In this article we present some nonexistence results concerning stable
solutions to the equation
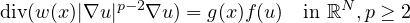
when f(u) is either
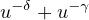 with
with
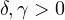 or
or
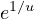 where w,g are suitable weight functions.
where w,g are suitable weight functions.
Submitted November 28, 2018. Published July 30, 2019.
Math Subject Classifications: 35A01, 35B93, 35J92.
Key Words: p-Laplacian; nonexistence; stable solution.
Show me the PDF file (344 KB), TEX file for this article.
 |
Kaushik Bal Department of Mathematics and Statistics Indian Institute of Technology Kanpur, UP-208016, India email: kaushik@iitk.ac.in |
|---|---|
 |
Prashanta Garain Department of Mathematics and Statistics Indian Institute of Technology Kanpur, UP-208016, India email: pgarain@iitk.ac.in |
Return to the EJDE web page