We consider a class of discrete nonlinear Schrodinger (DNLS) equations in m dimensional lattices with partially sublinear nonlinearity f. Combining variational methods and a priori estimate, we give a general sufficient condition on f for type (A), that is, a sequence of nontrivial homoclinic solutions accumulating to zero. By using a compact embedding technique, we overcome the loss of compactness due to the problem being set on the unbounded domain
.
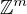Another obstacle caused by the local definition of f is solved by using
the cutoff methods to recover the global property of f.
To the best of our knowledge, this is the first time to obtain infinitely
many homoclinic solutions for the DNLS equations with partially sublinear
nonlinearity. Moreover, we prove that if f is not sublinear, the zero
solution is isolated from other homoclinic solutions.
Our results show that the sublinearity and oddness of f yield type (A).
Without the oddness assumption, we still can prove that this problem has
at least a nontrivial homoclinic solution if f is local sublinear, which
improves some existing results.
