In this article we consider the fractional Schrodinger-Poisson system
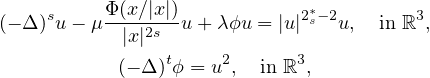
where
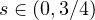 ,
,
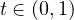 ,
,
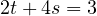 ,
,
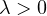 and
and
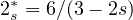 is the Sobolev critical exponent.
By using perturbation method, we establish the existence of a solution for
is the Sobolev critical exponent.
By using perturbation method, we establish the existence of a solution for
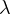 small enough.
small enough.
Yu Su, Haibo Chen, Senli Liu, Xianwen Fang
Abstract:
In this article we consider the fractional Schrodinger-Poisson system
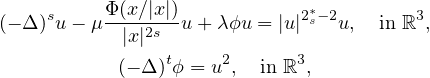
where
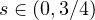 ,
,
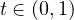 ,
,
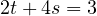 ,
,
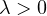 and
and
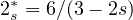 is the Sobolev critical exponent.
By using perturbation method, we establish the existence of a solution for
is the Sobolev critical exponent.
By using perturbation method, we establish the existence of a solution for
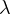 small enough.
small enough.
Submitted October 24, 2019. Published January 6, 2020.
Math Subject Classifications: 35B38, 35J47.
Key Words: Fractional Schrodinger-Poisson system; weighted Hardy potential;
critical exponent.
DOI: 10.58997/ejde.2020.01
Show me the PDF file (414 KB), TEX file for this article.
 |
Yu Su School of Mathematics and Big Data Anhui University of Science and Technology Huainan, 232001 Anhui, China email: yusumath@qq.com |
|---|---|
 |
Haibo Chen School of Mathematics and Statistics Central South University Changsha, 410083 Hunan, China email: math_chb@163.com |
 |
Senli Liu School of Mathematics and Statistics Central South University Changsha, 410083 Hunan, China email: jasonliu0615@163.com |
 |
Xianwen Fang School of Mathematics and Big Data Anhui University of Science and Technology Huainan, 232001 Anhui, China email: xwfang@aust.edu.cn |
Return to the EJDE web page