Electron. J. Differential Equations,
Vol. 2020 (2020), No. 02, pp. 1-10.
Lifespan of solutions of a fractional evolution equation with
higher order diffusion on the Heisenberg group
Ahmed Alsaedi, Bashir Ahmad, Mokhtar Kirane, Aberrazak Nabti
Abstract:
We consider the higher order diffusion Schrodinger equation with a time nonlocal
nonlinearity
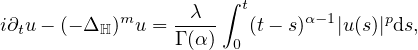
posed in
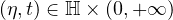 , supplemented with an initial
data
, supplemented with an initial
data
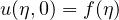 , where
, where
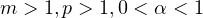 , and
, and
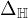 is the Laplacian operator on the
is the Laplacian operator on the
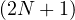 -dimensional Heisenberg group
-dimensional Heisenberg group
 .
Then, we prove a blow up result for its solutions. Furthermore, we give an upper
bound estimate of the life span of blow up solutions.
.
Then, we prove a blow up result for its solutions. Furthermore, we give an upper
bound estimate of the life span of blow up solutions.
Submitted June 8, 2019. Published January 7, 2020.
Math Subject Classifications: 35Q55, 35B44, 26A33, 35B30.
Key Words: Schrodinger equation; Heisenberg group; life span;
Riemann-Liouville fractional integrals and derivatives.
DOI: 10.58997/ejde.2020.02
Show me the PDF file (364 KB),
TEX file for this article.
 |
Ahmed Alsaedi
Nonlinear Analysis and Applied Mathematics (NAAM) Research Group
Faculty of Sciences
King Abdulaziz University
Jeddah 21589, Saudi Arabia
email: aalsaedi@hotmail.com
|
|---|
 |
Bashir Ahmad
Nonlinear Analysis and Applied Mathematics (NAAM) Research Group
Faculty of Sciences
King Abdulaziz University
Jeddah 21589, Saudi Arabia
email: bashirahmad_qau@yahoo.com
|
|---|
 |
Mokhtar Kirane
LASIE, Faculté des Sciences et Technologies
Université de La Rochelle
Avenue M. Crepeau, 17000
La Rochelle, France
email: mkirane@univ-lr.fr
|
|---|
 |
Abderrazak Nabti
Laboratoire de Mathématiques
Informatiques et Systèmes (LAMIS)
Université Larbi Tebessi
12002 Tebessa, Algeria
email: abderrazaknabti@gmail.com
|
|---|
Return to the EJDE web page
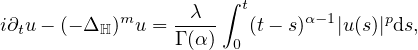
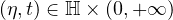 , supplemented with an initial
data
, supplemented with an initial
data
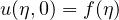 , where
, where
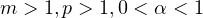 , and
, and
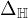 is the Laplacian operator on the
is the Laplacian operator on the
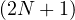 -dimensional Heisenberg group
-dimensional Heisenberg group
 .
Then, we prove a blow up result for its solutions. Furthermore, we give an upper
bound estimate of the life span of blow up solutions.
.
Then, we prove a blow up result for its solutions. Furthermore, we give an upper
bound estimate of the life span of blow up solutions.



