Electron. J. Differential Equations, Vol. 2020 (2020), No. 08, pp. 1-26.

Characterization of mean value harmonic functions on norm induced metric measure spaces with weighted Lebesgue measure

Antoni Kijowski

Abstract:
We study the mean-value harmonic functions on open subsets of~ 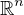$\mathbb{R}^n$ equipped with weighted Lebesgue measures and norm induced metrics. Our main result is a necessary condition stating that all such functions solve a certain homogeneous system of elliptic PDEs. Moreover, a converse result is established in case of analytic weights. Assuming the Sobolev regularity of the weight 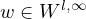$w \in W^{l,\infty}$ we show that strongly harmonic functions are also in 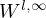$W^{l,\infty}$ and that they are analytic, whenever the weight is analytic.
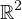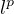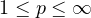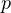The analysis is illustrated by finding all mean-value harmonic functions in $\mathbb{R}^2$ for the $l^p$-distance ${1 \leq p \leq \infty}$. The essential outcome is a certain discontinuity with respect to $p$ , i.e. that for all 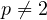$p \ne 2$ there are only finitely many linearly independent mean-value harmonic functions, while for p=2 there are infinitely many of them. 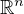We conclude with the remarkable observation that strongly harmonic functions in $\mathbb{R}^n$ possess the mean value property with respect to infinitely many weight functions obtained from a given weight.

Submitted March 21, 2019. Published January 14, 2020.
Math Subject Classifications: 31C05, 35J99, 30L99.
Key Words: Harmonic function; mean value property; metric measure space; Minkowski functional; norm induced metric; Pizzetti formula; weighted Lebesgue measure.
DOI: 10.58997/ejde.2020.08

Show me the PDF file (427 KB), TEX file for this article.

Antoni Kijowski
Institute of Mathematics
Polish Academy of Sciences, ul. Sniadeckich 8
00-656 Warsaw, Poland
email: akijowski@impan.pl

Return to the EJDE web page