Electron. J. Differential Equations, Vol. 2020 (2020), No. 103, pp. 1-34.
Time periodic solutions for the non-isentropic compressible quantum
hydrodynamic equations with viscosity in R^3
Min Li
Abstract:
This article concerns the existence and uniqueness of a time periodic solution
for the non-isentropic quantum hydrodynamic equations with viscosity.
By applying the Leray-Schauder theory, subtle energy estimates and a limiting method,
we obtain the existence of time periodic solutions under some smallness assumptions
on the time periodic external force in
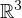 .
The uniqueness can be proved by similar energy estimates. In particular, the
quantum effects and the energy equation are taken into account in this paper which
play a significant role in the uniform (in the domain R and the positive constant
.
The uniqueness can be proved by similar energy estimates. In particular, the
quantum effects and the energy equation are taken into account in this paper which
play a significant role in the uniform (in the domain R and the positive constant
 ) estimates, especially in the selection of the norm.
) estimates, especially in the selection of the norm.
Submitted March 29, 2020. Published October 2, 2020.
Math Subject Classifications: 47H11, 35B10, 76Y05, 35Q35, 35G25, 76N10.
Key Words: Time periodic solutions; uniform energy estimates;
full quantum hydrodynamic equations with viscosity;
Leray-Schauder degree theory.
DOI: 10.58997/ejde.2020.103
Show me the PDF file (437 KB),
TEX file for this article.
 |
Min Li
Faculty of Applied Mathematics
Shanxi University of Finance and Economics
Taiyuan 030006, China
email: minlisxcj@163.com
|
|---|
Return to the EJDE web page
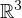 .
The uniqueness can be proved by similar energy estimates. In particular, the
quantum effects and the energy equation are taken into account in this paper which
play a significant role in the uniform (in the domain R and the positive constant
.
The uniqueness can be proved by similar energy estimates. In particular, the
quantum effects and the energy equation are taken into account in this paper which
play a significant role in the uniform (in the domain R and the positive constant
 ) estimates, especially in the selection of the norm.
) estimates, especially in the selection of the norm.
