In a recent book co-authored by the authors of this article, we studied by semigroup theory methods several classical evolution equations, including the heat and Laplace equations, with real time variable and complex spatial variable, under the hypothesis that the boundary function belongs to the space of analytic functions in the open unit disk and continuous in the closed unit disk, endowed with the uniform norm. Also, in a subsequent paper, the authors have extended the results for the heat and Laplace equations in weighted Bergman spaces on the unit disk. The purpose of this article is to show that the semigroup theory methods work for these two evolution equations of complex spatial variables, under the hypothesis that the boundary function belongs to the weighted Fock space on
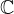 ,
,
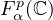 , with
, with
 , endowed with the
, endowed with the
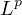 -norm. Also, the case of several complex variables is considered. The
proofs use the Jensen's inequality, Fubini's theorem for integrals and the
-norm. Also, the case of several complex variables is considered. The
proofs use the Jensen's inequality, Fubini's theorem for integrals and the
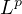 -integral modulus of continuity.
-integral modulus of continuity.

