Electron. J. Differential Equations, Vol. 2020 (2020), No. 110, pp. 1-28.
Existence of global solutions and blow-up of solutions for coupled systems
of fractional diffusion equations
Bashir Ahmad, Ahmed Alsaedi, Mohamed Berbiche, Mokhtar Kirane
Abstract:
We study the Cauchy problem for a system of semi-linear coupled
fractional-diffusion equations with polynomial nonlinearities posed in
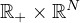 . Under appropriate conditions on the
exponents and the orders of the fractional time derivatives, we present a
critical value of the dimension N, for which global solutions with small
data exist, otherwise solutions blow-up in finite time. Furthermore, the
large time behavior of global solutions is discussed.
. Under appropriate conditions on the
exponents and the orders of the fractional time derivatives, we present a
critical value of the dimension N, for which global solutions with small
data exist, otherwise solutions blow-up in finite time. Furthermore, the
large time behavior of global solutions is discussed.
Submitted May 1, 2019. Published November 2, 2020.
Math Subject Classifications: 35A01, 35R09, 35K10, 45K05.
Key Words: Coupled fractional-diffusion equations; polynomial nonlinearities;
global solution; blow-up.
DOI: 10.58997/ejde.2020.110
Show me the PDF file (425 KB),
TEX file for this article.
 |
Bashir Ahmad
NAAM Research Group, Department of Mathematics
Faculty of Science
King Abdulaziz University, P.O. Box 80203
Jeddah 21589, Saudi Arabia
email: bashirahmad_qau@yahoo.com
|
|---|
 |
Ahmed Alsaedi
NAAM Research Group, Department of Mathematics
Faculty of Science
King Abdulaziz University, P.O. Box 80203
Jeddah 21589, Saudi Arabia
email: aalsaedi@hotmail.com
|
|---|
 |
Mohamed Berbiche
Laboratory of Mathematical Analysis,
Probability and Optimizations
Mohamed Khider University, Biskra, PO. Box 145
Biskra (07000) Algeria
email: berbichemed@yahoo.fr, mohamed.berbiche@univ-biskra.dz
|
|---|
 |
Mokhtar Kirane
Department of Mathematics and Statistics
College of Art and Sciences
Khalifa University of Science and Technology
Abu Dhabi, United Arab Emirates
email: mokhtar.kirane@ku.ac.ae, mokhtar.kirane@univ-lr.fr
|
|---|
Return to the EJDE web page
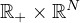 . Under appropriate conditions on the
exponents and the orders of the fractional time derivatives, we present a
critical value of the dimension N, for which global solutions with small
data exist, otherwise solutions blow-up in finite time. Furthermore, the
large time behavior of global solutions is discussed.
. Under appropriate conditions on the
exponents and the orders of the fractional time derivatives, we present a
critical value of the dimension N, for which global solutions with small
data exist, otherwise solutions blow-up in finite time. Furthermore, the
large time behavior of global solutions is discussed.



