Electron. J. Differential Equations, Vol. 2020 (2020), No. 118, pp. 1-25.
Polyharmonic systems involving critical nonlinearities with sign-changing weight functions
Anu Rani, Sarika Goyal
Abstract:
This article concerns the existence of multiple solutions of the
polyharmonic system involving critical nonlinearities with sign-changing
weight functions
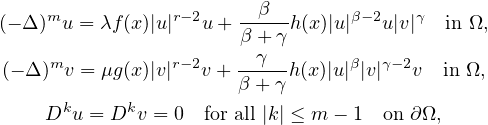
where
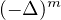 denotes the polyharmonic operators,
denotes the polyharmonic operators,
 is a bounded domain in
is a bounded domain in
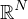 with smooth boundary
with smooth boundary
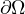 ,
,
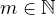 ,
,
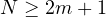 ,
,
 and
and
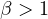 ,
,
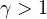 satisfying
satisfying
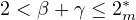 with
with
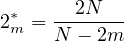 as a critical Sobolev exponent and
as a critical Sobolev exponent and
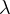 ,
,
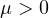 .
The functions f, g and
.
The functions f, g and
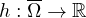 are sign-changing
weight functions satisfying f,
are sign-changing
weight functions satisfying f,
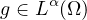 and
and
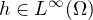 respectively. Using the variational methods and Nehari manifold, we prove that the
system admits at least two nontrivial solutions with respect to parameter
respectively. Using the variational methods and Nehari manifold, we prove that the
system admits at least two nontrivial solutions with respect to parameter
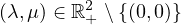 .
.
Submitted August 31, 2020. Published December 10, 2020.
Math Subject Classifications: 35A15, 35B33, 35J91.
Key Words: Polyharmonic operator system; sign-changing weight functions;
critical exponent; Nehari manifold; concave-convex nonlinearities.
DOI: 10.58997/ejde.2020.119
Show me the PDF file (445 KB),
TEX file for this article.
| |
Anu Rani
Department of Mathematics
Bennett University
Greater Noida, Uttar Pradesh, India
email: ar4091@bennett.edu.in
|
|---|
 |
Sarika Goyal
Department of Mathematics
Bennett University
Greater Noida, Uttar Pradesh, India
email: sarika1.iitd@gmail.com
|
|---|
Return to the EJDE web page
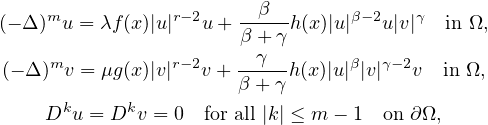
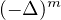 denotes the polyharmonic operators,
denotes the polyharmonic operators,
 is a bounded domain in
is a bounded domain in
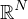 with smooth boundary
with smooth boundary
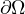 ,
,
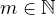 ,
,
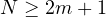 ,
,
 and
and
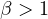 ,
,
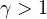 satisfying
satisfying
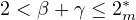 with
with
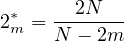 as a critical Sobolev exponent and
as a critical Sobolev exponent and
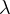 ,
,
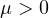 .
The functions f, g and
.
The functions f, g and
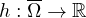 are sign-changing
weight functions satisfying f,
are sign-changing
weight functions satisfying f,
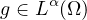 and
and
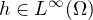 respectively. Using the variational methods and Nehari manifold, we prove that the
system admits at least two nontrivial solutions with respect to parameter
respectively. Using the variational methods and Nehari manifold, we prove that the
system admits at least two nontrivial solutions with respect to parameter
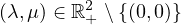 .
.
