Electron. J. Differential Equations, Vol. 2020 (2020), No. 122, pp. 1-14.
Existence and boundedness of solutions for a Keller-Segel system with
gradient dependent chemotactic sensitivity
Jianlu Yan, Yuxiang Li
Abstract:
We consider the Keller-Segel system with gradient dependent chemotactic sensitivity

in a smooth bounded domain
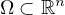 ,
,
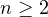 .
We shown that for all reasonably regular initial data
.
We shown that for all reasonably regular initial data
 and
and
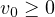 ,
the corresponding Neumann initial-boundary value problem possesses a global weak
solution which is uniformly bounded provided that
,
the corresponding Neumann initial-boundary value problem possesses a global weak
solution which is uniformly bounded provided that
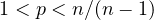 .
.
Submitted June 4, 2019. Published December 16. 2020.
Math Subject Classifications: 35K55, 35B40, 35Q92, 92C17.
Key Words: Keller-Segel system; weak solution; chemotactic sensitivity.
DOI: 10.58997/ejde.2020.122
Show me the PDF file (367 KB),
TEX file for this article.
 |
Jianlu Yan
Institute for Applied Mathematics
School of Mathematics
Southeast University
Nanjing 211189, China
email: 230159430@seu.edu.cn
|
|---|
 |
Yuxiang Li
Institute for Applied Mathematics
School of Mathematics
Southeast University
Nanjing 211189, China
email: lieyx@seu.edu.cn
|
|---|
Return to the EJDE web page

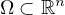 ,
,
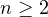 .
We shown that for all reasonably regular initial data
.
We shown that for all reasonably regular initial data
 and
and
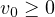 ,
the corresponding Neumann initial-boundary value problem possesses a global weak
solution which is uniformly bounded provided that
,
the corresponding Neumann initial-boundary value problem possesses a global weak
solution which is uniformly bounded provided that
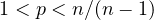 .
.

