Electron. J. Differential Equations, Vol. 2020 (2020), No. 123, pp. 1-13.
Existence and uniqueness of weak solutions to parabolic problems with
nonstandard growth and cross diffusion
Gurusamy Arumugam, Andre H. Erhardt
Abstract:
We establish the existence and uniqueness of weak solutions to the parabolic system with
nonstandard growth condition and cross diffusion,
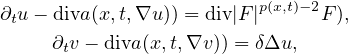
where
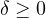 and
and
 denote the partial derivative of u
and v with respect to the time variable t, while
denote the partial derivative of u
and v with respect to the time variable t, while
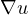 and
and
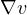 denote
the one with respect to the spatial variable x. Moreover, the vector field
denote
the one with respect to the spatial variable x. Moreover, the vector field
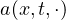 satisfies certain nonstandard p(x,t) growth, monotonicity and coercivity conditions.
satisfies certain nonstandard p(x,t) growth, monotonicity and coercivity conditions.
Submitted September 18, 2019. Published December 17, 2020.
Math Subject Classifications: 35A01, 35D30, 35K65.
Key Words: Nonlinear parabolic problem; nonstandard growth; cross diffusion.
DOI: 10.58997/ejde.2020.123
Show me the PDF file (367 KB),
TEX file for this article.
 |
Gurusamy Arumugam
Discipline of Mathematics
Indian Institute of Technology Gandhinagar
Gandhinagar, 382355 Gujarat, India
email: gurusamy.a@iitgn.ac.in, guru.poy@gmail.com
|
|---|
 |
André H. Erhardt
Department of Mathematics
University of Oslo, P.O. Box 1053 Blindern
N-0316 Oslo, Norway
email: andreerh@math.uio.no
|
|---|
Return to the EJDE web page
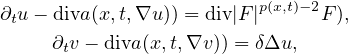
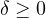 and
and
 denote the partial derivative of u
and v with respect to the time variable t, while
denote the partial derivative of u
and v with respect to the time variable t, while
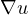 and
and
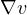 denote
the one with respect to the spatial variable x. Moreover, the vector field
denote
the one with respect to the spatial variable x. Moreover, the vector field
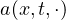 satisfies certain nonstandard p(x,t) growth, monotonicity and coercivity conditions.
satisfies certain nonstandard p(x,t) growth, monotonicity and coercivity conditions.

