Achache Mahdi, Tebbani Hossni
Abstract:
We consider the regularity for the non-autonomous Cauchy problem
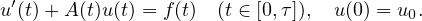
The time dependent operator A(t) is associated with
(time dependent) sesquilinear forms on a Hilbert space
.
We prove the maximal regularity result in temporally weighted L^2-spaces
and other regularity properties for the solution of the problem under minimal
regularity assumptions on the forms and the initial value u_0.
Our results are motivated by boundary value problems.
Submitted October 9, 2019. Published December 20, 2020.
Math Subject Classifications: 35A23.
Key Words: Maximal regularity; non-autonomous evolution equation; weighted space.
DOI: 10.58997/ejde.2020.124
Show me the PDF file (415 KB), TEX file for this article.
 |
Achache Mahdi Department of Mathematics, Univ. Bordeaux Institut de Mathématiques (IMB). CNRS UMR 5251. 351 Cours de la Libération 33405 Talence, France email: Mahdi.Achache@math.ubordeaux.fr |
|---|---|
 |
Tebbani Hossni Department of Mathematics Univ. Séetif -1-, Algeria email maths47@ymail.com |
Return to the EJDE web page