This article concerns the Caputo fractional differential equation
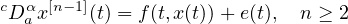
where
![$x ^{[n-1]}$](images/a1x.png) is the quasiderivative of x of order (n-1) and
is the quasiderivative of x of order (n-1) and
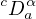 is the Caputo derivative of the order
is the Caputo derivative of the order
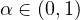 .
We study the continuability and noncontinuability of solutions.
.
We study the continuability and noncontinuability of solutions.
Miroslav Bartusek
Abstract:
This article concerns the Caputo fractional differential equation
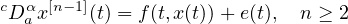
where
![$x ^{[n-1]}$](images/a1x.png) is the quasiderivative of x of order (n-1) and
is the quasiderivative of x of order (n-1) and
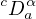 is the Caputo derivative of the order
is the Caputo derivative of the order
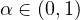 .
We study the continuability and noncontinuability of solutions.
.
We study the continuability and noncontinuability of solutions.
Submitted September 15, 2019. Published December 22, 2020.
Math Subject Classifications: 26A33, 34A08.
Key Words: Caputo fractional equations; continuability; noncontinuability; quasiderivatives.
DOI: 10.58997/ejde.2020.128
Show me the PDF file (342 KB), TEX file for this article.
 |
Miroslav Bartusek Department of Mathematics and Statistics Masaryk University 611 37 Brno, Czech Republic email: bartusek@math.muni.cz |
|---|
Return to the EJDE web page