Electron. J. Differential Equations, Vol. 2020 (2020), No. 130, pp. 1-17.
Schrodinger-Poisson systems with singular potential and critical exponent
Senli Liu, Haibo Chen, Zhaosheng Feng
Abstract:
In this article we study the Schrodinger-Poisson system
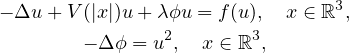
where V is a singular potential with the parameter
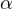 and the nonlinearity f
satisfies critical growth. By applying a generalized version of Lions-type theorem and
the Nehari manifold theory, we establish the existence of the nonnegative ground state
solution when
and the nonlinearity f
satisfies critical growth. By applying a generalized version of Lions-type theorem and
the Nehari manifold theory, we establish the existence of the nonnegative ground state
solution when
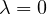 .
By the perturbation method, we obtain a nontrivial solution to above system when
.
By the perturbation method, we obtain a nontrivial solution to above system when
 .
.
Submitted July 18, 2020. Published December 26, 2020.
Math Subject Classifications: 35J20, 35J75, 35Q55.
Key Words: Schrodinger-Poisson system; Lions-type theorem;
singular potential; ground state solution; critical exponent.
Show me the PDF file (388 KB),
TEX file for this article.
 |
Senli Liu
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: mathliusl@csu.edu.cn
|
|---|
 |
Haibo Chen
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: math_chb@163.com
|
|---|
 |
Zhaosheng Feng
School of Mathematical and Statistical Sciences
University of Texas Rio Grande Valley
Edinburg, TX 78539, USA
email: zhaosheng.feng@utrgv.edu
|
|---|
Return to the EJDE web page
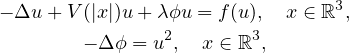
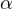 and the nonlinearity f
satisfies critical growth. By applying a generalized version of Lions-type theorem and
the Nehari manifold theory, we establish the existence of the nonnegative ground state
solution when
and the nonlinearity f
satisfies critical growth. By applying a generalized version of Lions-type theorem and
the Nehari manifold theory, we establish the existence of the nonnegative ground state
solution when
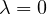 .
By the perturbation method, we obtain a nontrivial solution to above system when
.
By the perturbation method, we obtain a nontrivial solution to above system when
 .
.


