Electron. J. Differential Equations, Vol. 2020 (2020), No. 19, pp. 1-14.
Piecewise linear differential systems with an algebraic line of separation
Armengol Gasull, Joan Torregrosa, Xiang Zhang
Abstract:
We study the number of limit cycles of planar piecewise linear differential
systems separated by a branch of an algebraic curve. We show that for each
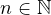 there exist piecewise linear differential systems separated by
an algebraic curve of degree n having [n/2] hyperbolic limit cycles.
Moreover, when n=2,3, we study in more detail the problem, considering
a perturbation of a center and constructing examples with 4 and 5 limit cycles,
respectively. These results follow by proving that the set of functions
generating the first order averaged function associated to the problem is an
extended complete Chebyshev system in a suitable interval.
there exist piecewise linear differential systems separated by
an algebraic curve of degree n having [n/2] hyperbolic limit cycles.
Moreover, when n=2,3, we study in more detail the problem, considering
a perturbation of a center and constructing examples with 4 and 5 limit cycles,
respectively. These results follow by proving that the set of functions
generating the first order averaged function associated to the problem is an
extended complete Chebyshev system in a suitable interval.
Submitted April 23, 2018. Published February 14, 2020.
Math Subject Classifications: 34C25, 34C07, 37G15.
Key Words: Piecewise linear differential system;
algebraic separation; limit cycle; ECT-system.
DOI: 10.58997/ejde.2020.19
Show me the PDF file (331 KB),
TEX file for this article.
 |
Armengol Gasull
Departament de Matemàtiques
Universitat Autònoma de Barcelona
08193 Bellaterra, Barcelona, Catalonia, Spain
email: gasull@mat.uab.cat
|
|---|
 |
Joan Torregrosa
Departament de Matemàtiques
Universitat Autònoma de Barcelona
08193 Bellaterra, Barcelona, Catalonia, Spain
email: torre@mat.uab.cat
|
|---|
 |
Xiang Zhang
School of Mathematical Sciences
Key Laboratory of Scientific and Engineering Computing
Shanghai Jiao Tong University
Shanghai 200240, China
email: xzhang@sjtu.edu.cn
|
|---|
Return to the EJDE web page
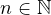 there exist piecewise linear differential systems separated by
an algebraic curve of degree n having [n/2] hyperbolic limit cycles.
Moreover, when n=2,3, we study in more detail the problem, considering
a perturbation of a center and constructing examples with 4 and 5 limit cycles,
respectively. These results follow by proving that the set of functions
generating the first order averaged function associated to the problem is an
extended complete Chebyshev system in a suitable interval.
there exist piecewise linear differential systems separated by
an algebraic curve of degree n having [n/2] hyperbolic limit cycles.
Moreover, when n=2,3, we study in more detail the problem, considering
a perturbation of a center and constructing examples with 4 and 5 limit cycles,
respectively. These results follow by proving that the set of functions
generating the first order averaged function associated to the problem is an
extended complete Chebyshev system in a suitable interval.


