Electron. J. Differential Equations, Vol. 2020 (2020), No. 21, pp. 1-17.
Maximum and antimaximum principles for the p-Laplacian with weighted
Steklov boundary conditions
Mabel Cuesta, Liamidi Leadi, Pascaline Nshimirimana
Abstract:
We study the maximum and antimaximum principles for the p-Laplacian
operator under Steklov boundary conditions with an indefinite weight
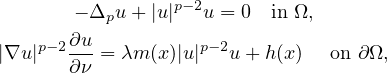
where
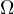 is a smooth bounded domain of
is a smooth bounded domain of
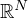 , N>1.
After reviewing some elementary properties of the principal eigenvalues of
the p-Laplacian under Steklov boundary conditions with an indefinite weight,
we investigate the maximum and antimaximum principles for this problem.
Also we give a characterization for the interval of the validity of the
uniform antimaximum principle.
, N>1.
After reviewing some elementary properties of the principal eigenvalues of
the p-Laplacian under Steklov boundary conditions with an indefinite weight,
we investigate the maximum and antimaximum principles for this problem.
Also we give a characterization for the interval of the validity of the
uniform antimaximum principle.
Submitted November 18, 2019. Published March 2, 2020.
Math Subject Classifications: 35J70.
Key Words: p-Laplacian; Steklov boundary conditions: indefinite weight;
maximum and antimaximum principles.
DOI: 10.58997/ejde.2020.21
Show me the PDF file (382 KB),
TEX file for this article.
 |
Mabel Cuesta
Université du Littoral ULCO, LMPA
50 rue F. Buisson 62220 Calais, France
email: mabel.cuesta@univ-littoral.fr
|
|---|
 |
Liamidi Leadi
Université d'Abomey Calavi, FAST, IMSP
Porto-Novo, Bénin
email: leadiare@imsp-uac.org
|
|---|
 |
Pascaline Nshimirimana
Université d'Abomey Calavi, FAST, IMSP
Porto-Novo, Bénin
email: pascaline.nshimirimana@imsp-uac.org
|
|---|
Return to the EJDE web page
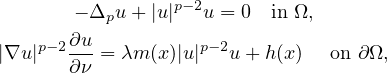
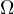 is a smooth bounded domain of
is a smooth bounded domain of
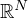 , N>1.
After reviewing some elementary properties of the principal eigenvalues of
the p-Laplacian under Steklov boundary conditions with an indefinite weight,
we investigate the maximum and antimaximum principles for this problem.
Also we give a characterization for the interval of the validity of the
uniform antimaximum principle.
, N>1.
After reviewing some elementary properties of the principal eigenvalues of
the p-Laplacian under Steklov boundary conditions with an indefinite weight,
we investigate the maximum and antimaximum principles for this problem.
Also we give a characterization for the interval of the validity of the
uniform antimaximum principle.


