Electron. J. Differential Equations, Vol. 2020 (2020), No. 24, pp. 1-10.
Almost optimal local well-posedness for modified Boussinesq equations
Dan-Andrei Geba, Bai Lin
Abstract:
In this article, we investigate a class of modified Boussinesq equations,
for which we provide first an alternate proof of local well-posedness in
the space
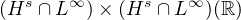 (
(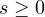 )
to the one obtained by Constantin and Molinet [7].
Secondly, we show that the associated flow map is not smooth when considered
from
)
to the one obtained by Constantin and Molinet [7].
Secondly, we show that the associated flow map is not smooth when considered
from
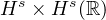 into
into
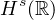 for s<0,
thus providing a threshold for the regularity needed to perform a Picard
iteration for these equations.
for s<0,
thus providing a threshold for the regularity needed to perform a Picard
iteration for these equations.
Submitted June 12, 2019. Published March 19, 2020.
Math Subject Classifications: 35B30, 35Q55.
Key Words: Modified Boussinesq equation; well-posedness; ill-posedness.
DOI: 10.58997/ejde.2020.24
Show me the PDF file (335 KB),
TEX file for this article.
 |
Dan-Andrei Geba
Department of Mathematics
University of Rochester
Rochester, NY 14627, USA
email: dangeba@math.rochester.edu
|
|---|
 |
Bai Lin
Department of Mathematics
University of Rochester
Rochester, NY 14627, USA
email: blin13@ur.rochester.edu
|
|---|
Return to the EJDE web page
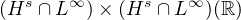 (
(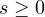 )
to the one obtained by Constantin and Molinet [7].
Secondly, we show that the associated flow map is not smooth when considered
from
)
to the one obtained by Constantin and Molinet [7].
Secondly, we show that the associated flow map is not smooth when considered
from
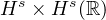 into
into
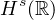 for s<0,
thus providing a threshold for the regularity needed to perform a Picard
iteration for these equations.
for s<0,
thus providing a threshold for the regularity needed to perform a Picard
iteration for these equations.

