Electron. J. Differential Equations, Vol. 2020 (2020), No. 26, pp. 1-18.
Null controllability from the exterior of fractional parabolic-elliptic
coupled systems
Carole Louis-Rose
Abstract:
We analyze the null controllability properties from the exterior of two
parabolic-elliptic coupled systems governed by the fractional Laplacian
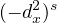 ,
,
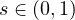 ,
in one space dimension. In each system, the control
is located on a non-empty open set of
,
in one space dimension. In each system, the control
is located on a non-empty open set of
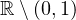 .
Using the spectral theory of the fractional Laplacian and a unique continuation
principle for the dual equation, we show that the problem is null controllable
if and only if 1/2<s<1.
.
Using the spectral theory of the fractional Laplacian and a unique continuation
principle for the dual equation, we show that the problem is null controllable
if and only if 1/2<s<1.
Submitted April 5, 2019. Published March 27, 2020.
Math Subject Classifications: 93B05, 35R11, 93C05, 35C10, 93B60.
Key Words: Controllability; fractional partial differential equation;
linear system; series solution; eigenvalue problem.
DOI: 10.58997/ejde.2020.26
Show me the PDF file (369 KB),
TEX file for this article.
 |
Carole Louis-Rose
Université des Antilles
Département de Mathématiques et Informatique
laboratoire LAMIA, campus de Fouillole
97157 Pointe-à-Pitre, Guadeloupe
email: carole.louis-rose@univ-antilles.fr
|
|---|
Return to the EJDE web page
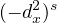 ,
,
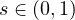 ,
in one space dimension. In each system, the control
is located on a non-empty open set of
,
in one space dimension. In each system, the control
is located on a non-empty open set of
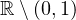 .
Using the spectral theory of the fractional Laplacian and a unique continuation
principle for the dual equation, we show that the problem is null controllable
if and only if 1/2<s<1.
.
Using the spectral theory of the fractional Laplacian and a unique continuation
principle for the dual equation, we show that the problem is null controllable
if and only if 1/2<s<1.
