Electron. J. Differential Equations, Vol. 2020 (2020), No. 30, pp. 1-12.
S-asymptotically omega-periodic mild solutions to fractional differential
equations
Darin Brindle, Gaston M. N'Guerekata
Abstract:
This article concerns the existence of mild solutions to the
semilinear fractional differential equation
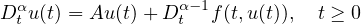
with nonlocal conditions
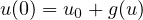 where
where
 (
(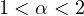 )
is the Riemann-Liouville derivative,
)
is the Riemann-Liouville derivative,
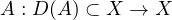 is a linear densely defined operator of sectorial type
on a complex Banach space
is a linear densely defined operator of sectorial type
on a complex Banach space
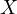 ,
,
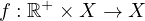 is S-asymptotically
is S-asymptotically
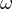 -periodic
with respect to the first variable.
We use the Krsnoselskii's theorem to prove our main theorem.
The results obtained are new even in the context of asymptotically
-periodic
with respect to the first variable.
We use the Krsnoselskii's theorem to prove our main theorem.
The results obtained are new even in the context of asymptotically
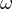 -periodic
functions. An application to fractional relaxation-oscillation equations is given.
-periodic
functions. An application to fractional relaxation-oscillation equations is given.
Submitted August 11, 2019. Published April 7, 2020.
Math Subject Classifications: 34G20, 34G10.
Key Words: S-asymptotically omega-periodic sequence;
fractional semilinear differential equation.
An addendum was posted on April 18, 2020. It corrects Theorem 2.9 and its proof. See the last page of this article.
DOI: 10.58997/ejde.2020.30
Show me the PDF file (358 KB),
TEX file for this article.
 |
Darin Brindle
Department of Mathematics
Morgan State University
Baltimore, MD 21251, USA
email: Darin.Brindle@morgan.edu
|
|---|
 |
Gaston M. N'Guérékata
Department of Mathematics
Morgan State University
Baltimore, MD 21251, USA
email: Gaston.N'Guerekata@morgan.edu
|
|---|
Return to the EJDE web page
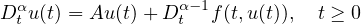
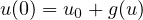 where
where
 (
(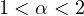 )
is the Riemann-Liouville derivative,
)
is the Riemann-Liouville derivative,
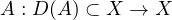 is a linear densely defined operator of sectorial type
on a complex Banach space
is a linear densely defined operator of sectorial type
on a complex Banach space
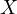 ,
,
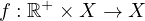 is S-asymptotically
is S-asymptotically
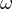 -periodic
with respect to the first variable.
We use the Krsnoselskii's theorem to prove our main theorem.
The results obtained are new even in the context of asymptotically
-periodic
with respect to the first variable.
We use the Krsnoselskii's theorem to prove our main theorem.
The results obtained are new even in the context of asymptotically
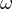 -periodic
functions. An application to fractional relaxation-oscillation equations is given.
-periodic
functions. An application to fractional relaxation-oscillation equations is given.

