Electron. J. Differential Equations, Vol. 2020 (2020), No. 35, pp. 1-11.
Existence and uniqueness of the p-generalized modified error function
Julieta Bollati, Jose A. Semitiel, Maria F. Natale, Domingo A. Tarzia
Abstract:
In this article, we define a p-generalized modified error function as the solution
to a non-linear ordinary differential equation of second order, with a Robin type
boundary condition at x=0. We prove existence and uniqueness of a non-negative
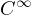 solution by using a fixed point argument.
We show that the p-generalized modified error function converges to the p-modified
error function defined as the solution to a similar problem with a Dirichlet
boundary condition.
In both problems, for p=1, the generalized modified error function and the modified
error function are recovered.
In addition, we analyze the existence and uniqueness of solution to a problem with
a Neumann boundary condition.
solution by using a fixed point argument.
We show that the p-generalized modified error function converges to the p-modified
error function defined as the solution to a similar problem with a Dirichlet
boundary condition.
In both problems, for p=1, the generalized modified error function and the modified
error function are recovered.
In addition, we analyze the existence and uniqueness of solution to a problem with
a Neumann boundary condition.
Submitted April 19, 2019. Published April 18, 2020.
Math Subject Classifications: 34A34, 47H10, 33E30, 34A12, 35R35.
Key Words: Modified error function; generalized modified error function;
nonlinear ordinary differential equation; Banach fixed point theorem;
Stefan problem.
DOI: 10.58997/ejde.2020.35
Show me the PDF file (325 KB),
TEX file for this article.
 |
Julieta Bollati
CONICET, Argentina.
Depto. Matemática, FCE, Univ. Austral
Paraguay 1950,
S2000FZF Rosario, Argentina
email: jbollati@austral.edu.ar
|
|---|
 |
José A. Semitiel
Depto. Matemática, FCE, Univ. Austral
Paraguay 1950, S2000FZF Rosario, Argentina
email: jsemitiel@austral.edu.ar
|
|---|
 |
María F. Natale
Depto. Matemática, FCE, Univ. Austral
Paraguay 1950, S2000FZF Rosario, Argentina
email: fnatale@austral.edu.ar
|
|---|
 |
Domingo A. Tarzia
CONICET, Argentina.
Depto. Matemática, FCE, Univ. Austral
Paraguay 1950, S2000FZF Rosario, Argentina
email: dtarzia@austral.edu.ar
|
|---|
Return to the EJDE web page
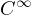 solution by using a fixed point argument.
We show that the p-generalized modified error function converges to the p-modified
error function defined as the solution to a similar problem with a Dirichlet
boundary condition.
In both problems, for p=1, the generalized modified error function and the modified
error function are recovered.
In addition, we analyze the existence and uniqueness of solution to a problem with
a Neumann boundary condition.
solution by using a fixed point argument.
We show that the p-generalized modified error function converges to the p-modified
error function defined as the solution to a similar problem with a Dirichlet
boundary condition.
In both problems, for p=1, the generalized modified error function and the modified
error function are recovered.
In addition, we analyze the existence and uniqueness of solution to a problem with
a Neumann boundary condition.



