Electron. J. Differential Equations, Vol. 2020 (2020), No. 40, pp. 1-18.
Complex Ginzburg-Landau equations with a delayed nonlocal perturbation
Jesus Ildefonso Diaz, Juan Francisco Padial, Jose Ignacio Tello, Lourdes Tello
Abstract:
We consider an initial boundary value problem of the complex Ginzburg-Landau
equation with some delayed feedback terms proposed for the control of chemical
turbulence in reaction diffusion systems.
We consider the equation in a bounded domain
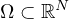 (
(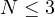 ),
),
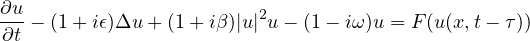
for t>0, with
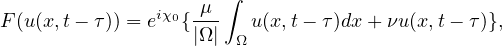
where
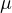 ,
,
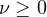 ,
,
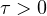 but the rest of real parameters
but the rest of real parameters
 ,
,
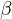 ,
,
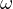 and
and
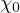 do not have a prescribed sign. We prove the
existence and uniqueness of weak solutions of problem for a range of initial
data and parameters. When
do not have a prescribed sign. We prove the
existence and uniqueness of weak solutions of problem for a range of initial
data and parameters. When
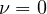 and
and
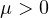 we prove that only the initial
history of the integral on
we prove that only the initial
history of the integral on
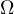 of the unknown on
of the unknown on
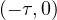 and a
standard initial condition at t=0 are required to determine univocally the
existence of a solution. We prove several qualitative properties of solutions,
such as the finite extinction time (or the zero exact controllability) and the
finite speed of propagation, when the term
and a
standard initial condition at t=0 are required to determine univocally the
existence of a solution. We prove several qualitative properties of solutions,
such as the finite extinction time (or the zero exact controllability) and the
finite speed of propagation, when the term
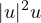 is replaced by
is replaced by
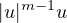 , for some
, for some
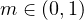 .
We extend
to the delayed case some previous results in the literature of complex
equations without any delay.
.
We extend
to the delayed case some previous results in the literature of complex
equations without any delay.
Submitted March 31, 2020. Published April 30, 2020.
Math Subject Classifications: 35K15, 35B40, 35Q35.
Key Words: Complex Ginzburg-Landau equation; nonlocal delayed perturbation;
existence of weak solutions; uniqueness; qualitative properties.
Show me the PDF file (402 KB),
TEX file for this article.
 |
J. Ildefonso Díaz
Instituto de Matemática Interdisciplinar
Universidad Complutense de Madrid
28040 Madrid, Spain
email: jidiaz@ucm.es
|
|---|
 |
J. Francisco Padial
Departamento de Matemática Aplicada
E.T.S. de arquitectura
Universidad Politécnica de Madrid
28040 Madrid, Spain
email: jf.padial@upm.es
|
|---|
 |
J. Ignacio Tello
Departamento de Matemáticas Fundametales
Facultad de Ciencias
Universidad Nacional de Educación a Distancia
28040 Madrid, Spain
email: jtello@mat.uned.es
|
|---|
 |
Lourdes Tello
Departamento de Matemática Aplicada
E.T.S. de arquitectura
Universidad Politécnica de Madrid
28040 Madrid, Spain
email: l.tello@upm.es
|
|---|
Return to the EJDE web page
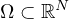 (
(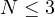 ),
),
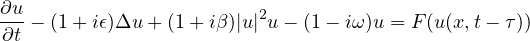
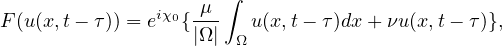
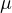 ,
,
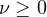 ,
,
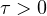 but the rest of real parameters
but the rest of real parameters
 ,
,
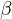 ,
,
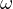 and
and
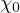 do not have a prescribed sign. We prove the
existence and uniqueness of weak solutions of problem for a range of initial
data and parameters. When
do not have a prescribed sign. We prove the
existence and uniqueness of weak solutions of problem for a range of initial
data and parameters. When
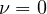 and
and
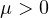 we prove that only the initial
history of the integral on
we prove that only the initial
history of the integral on
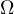 of the unknown on
of the unknown on
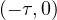 and a
standard initial condition at t=0 are required to determine univocally the
existence of a solution. We prove several qualitative properties of solutions,
such as the finite extinction time (or the zero exact controllability) and the
finite speed of propagation, when the term
and a
standard initial condition at t=0 are required to determine univocally the
existence of a solution. We prove several qualitative properties of solutions,
such as the finite extinction time (or the zero exact controllability) and the
finite speed of propagation, when the term
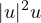 is replaced by
is replaced by
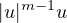 , for some
, for some
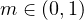 .
We extend
to the delayed case some previous results in the literature of complex
equations without any delay.
.
We extend
to the delayed case some previous results in the literature of complex
equations without any delay.



