Electron. J. Differential Equations, Vol. 2020 (2020), No. 50, pp. 1-19.
Mathematical methods for the randomized non-autonomous Bertalanffy model
Julia Calatayud, Tomas Caraballo, Juan Carlos Cortes, Marc Jornet
Abstract:
In this article we analyze the randomized non-autonomous Bertalanffy model
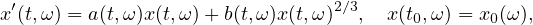
where
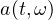 and
and
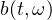 are stochastic processes and
are stochastic processes and
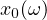 is a random variable, all of them defined in an underlying complete probability space.
Under certain assumptions on a, b and
is a random variable, all of them defined in an underlying complete probability space.
Under certain assumptions on a, b and
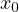 , we obtain a solution stochastic process,
, we obtain a solution stochastic process,
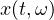 , both in the sample path and in the mean square senses.
By using the random variable transformation technique and Karhunen-Loeve expansions,
we construct a sequence of probability density functions that under certain conditions
converge pointwise or uniformly to the density function of
, both in the sample path and in the mean square senses.
By using the random variable transformation technique and Karhunen-Loeve expansions,
we construct a sequence of probability density functions that under certain conditions
converge pointwise or uniformly to the density function of
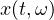 ,
,
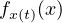 .
This permits approximating the expectation and the variance of
.
This permits approximating the expectation and the variance of
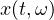 .
At the end, numerical experiments are carried out to put in
practice our theoretical findings.
.
At the end, numerical experiments are carried out to put in
practice our theoretical findings.
Submitted July 20, 2019. Published May 26, 2020.
Math Subject Classifications: 34F05, 60H35, 60H10, 65C30.
Key Words: Random non-autonomous Bertalanffy model;
random differential equation; random variable transformation technique;
Karhunen-Loeve expansion; probability density function.
DOI: 10.58997/ejde.2020.50
Show me the PDF file (542 KB),
TEX file for this article.
 |
Julia Calatayud
Instituto Universitario de Matemática Multidisciplinar
Universitat Politècnica de València
Camino de Vera s/n, 46022
Valencia, Spain
email: jucagre@doctor.upv.es
|
|---|
 |
Tomás Caraballo
Dpto. Ecuaciones Diferenciales y Análisis Numérico
Universidad de Sevilla
c/ Tarfia s/n, 41012
Sevilla, Spain
email: caraball@us.es
|
|---|
 |
Juan Carlos Cortés
Instituto Universitario de Matemática Multidisciplinar
Universitat Politècnica de València
Camino de Vera s/n, 46022
Valencia, Spain
email: jccortes@imm.upv.es
|
|---|
 |
Marc Jornet
Instituto Universitario de Matemática Multidisciplinar
Universitat Politècnica de València
Camino de Vera s/n, 46022
Valencia, Spain
email: marjorsa@doctor.upv.es
|
|---|
Return to the EJDE web page
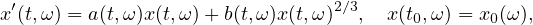
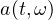 and
and
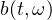 are stochastic processes and
are stochastic processes and
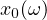 is a random variable, all of them defined in an underlying complete probability space.
Under certain assumptions on a, b and
is a random variable, all of them defined in an underlying complete probability space.
Under certain assumptions on a, b and
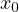 , we obtain a solution stochastic process,
, we obtain a solution stochastic process,
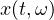 , both in the sample path and in the mean square senses.
By using the random variable transformation technique and Karhunen-Loeve expansions,
we construct a sequence of probability density functions that under certain conditions
converge pointwise or uniformly to the density function of
, both in the sample path and in the mean square senses.
By using the random variable transformation technique and Karhunen-Loeve expansions,
we construct a sequence of probability density functions that under certain conditions
converge pointwise or uniformly to the density function of
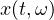 ,
,
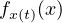 .
This permits approximating the expectation and the variance of
.
This permits approximating the expectation and the variance of
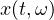 .
At the end, numerical experiments are carried out to put in
practice our theoretical findings.
.
At the end, numerical experiments are carried out to put in
practice our theoretical findings.



