Electron. J. Differential Equations, Vol. 2020 (2020), No. 53, pp. 1-18.
Traveling wave solutions for fully parabolic Keller-Segel chemotaxis
systems with a logistic source
Rachidi B. Salako, Wenxian Shen
Abstract:
This article concerns traveling wave solutions of the fully parabolic Keller-Segel
chemotaxis system with logistic source,
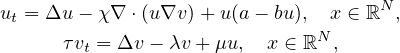
where
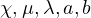 are positive numbers, and
are positive numbers, and
 .
Among others, it is proved that if
.
Among others, it is proved that if
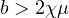 and
and
 ,
then for every
,
then for every
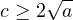 ,
this system has a traveling wave solution
,
this system has a traveling wave solution
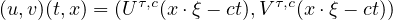 (for all
(for all
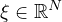 )
connecting the two constant steady states
)
connecting the two constant steady states
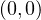 and
and
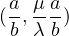 ,
and there is no such solutions with speed
,
and there is no such solutions with speed
 less than
less than
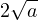 ,
which improves the results established in [30]
and shows that this system has a minimal wave speed
,
which improves the results established in [30]
and shows that this system has a minimal wave speed
 ,
which is independent of the chemotaxis.
,
which is independent of the chemotaxis.
Submitted August 11, 2019. Published May 27, 2020.
Math Subject Classifications: 35B35, 35B40, 35K57, 35Q92, 92C17.
Key Words: Parabolic chemotaxis system; logistic source; traveling wave solution;
minimal wave speed.
DOI: 10.58997/ejde.2020.53
Show me the PDF file (410 KB),
TEX file for this article.
 |
Rachidi B. Salako
Department of Mathematics
The Ohio State University
Columbus, OH 43210-1174, USA
email: salako.7@osu.edu
|
|---|
 |
Wenxian Shen
Department of Mathematics and Statistics
Auburn University
Auburn, AL 36849, USA
email: wenxish@auburn.edu
|
|---|
Return to the EJDE web page
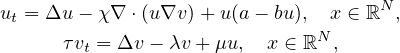
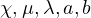 are positive numbers, and
are positive numbers, and
 .
Among others, it is proved that if
.
Among others, it is proved that if
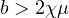 and
and
 ,
then for every
,
then for every
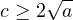 ,
this system has a traveling wave solution
,
this system has a traveling wave solution
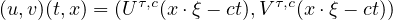 (for all
(for all
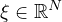 )
connecting the two constant steady states
)
connecting the two constant steady states
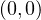 and
and
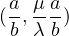 ,
and there is no such solutions with speed
,
and there is no such solutions with speed
 less than
less than
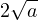 ,
which improves the results established in [30]
and shows that this system has a minimal wave speed
,
which improves the results established in [30]
and shows that this system has a minimal wave speed
 ,
which is independent of the chemotaxis.
,
which is independent of the chemotaxis.

