Electron. J. Differential Equations, Vol. 2020 (2020), No. 54, pp. 1-17.

Low regularity of non-L^2(R^n) local solutions to gMHD-alpha systems

Lorenzo Riva, Nathan Pennington

Abstract:
The Magneto-Hydrodynamic (MHD) system of equations governs viscous fluids subject to a magnetic field and is derived via a coupling of the Navier-Stokes equations and Maxwell's equations. Recently it has become common to study generalizations of fluids-based differential equations. Here we consider the generalized Magneto-Hydrodynamic alpha (gMHD-$\alpha$) system, which differs from the original MHD system by including an additional non-linear terms (indexed by $\alpha$), and replacing the Laplace operators by more general Fourier multipliers with symbols of the form 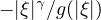$-|\xi|^\gamma / g(|\xi|)$. 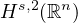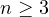In [8], the problem was considered with initial data in the Sobolev space $H^{s,2}(\mathbb{R}^n)$ with $n \geq 3$. 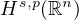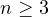Here we consider the problem with initial data in $H^{s,p}(\mathbb{R}^n)$ with $n \geq 3$ and $p > 2$. Our goal is to minimizing the regularity required for obtaining uniqueness of a solution.

Submitted July 31, 2019. Published May 28. 2020.
Math Subject Classifications: 35B65, 35A02, 76W05.
Key Words: Generalized MHD-alpha; local solution; low regularity.
DOI: 10.58997/ejde.2020.54

Show me the PDF file (349 KB), TEX file for this article.

Lorenzo Riva
Creighton University
2500 California Plaza
Omaha, NE 68178, USA
email: LorenzoRiva@creighton.edu
Nathan Pennington
Creighton University
2500 California Plaza
Omaha, NE 68178, USA
email: NathanPennington@creighton.edu

Return to the EJDE web page