We study the global dynamics of the classic May-Leonard model in
 .
Such model depends on two real parameters and its global dynamics is known when
the system is completely integrable. Using the Poincare compactification on
.
Such model depends on two real parameters and its global dynamics is known when
the system is completely integrable. Using the Poincare compactification on
 we obtain the global dynamics of the classical May-Leonard differential
system in
we obtain the global dynamics of the classical May-Leonard differential
system in
 when
when
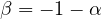 . In this case, the system is
non-integrable and it admits a Darboux invariant. We provide the global phase
portrait in each octant and in the Poincare ball, that is, the compactification
of
. In this case, the system is
non-integrable and it admits a Darboux invariant. We provide the global phase
portrait in each octant and in the Poincare ball, that is, the compactification
of
 in the sphere
in the sphere
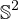 at infinity.
We also describe the
at infinity.
We also describe the
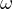 -limit and
-limit and
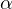 -limit of each of the orbits.
For some values of the parameter
-limit of each of the orbits.
For some values of the parameter
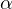 we find a separatrix cycle F formed
by orbits connecting the finite singular points on the boundary of the first octant
and every orbit on this octant has
we find a separatrix cycle F formed
by orbits connecting the finite singular points on the boundary of the first octant
and every orbit on this octant has
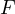 as the
as the
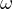 -limit.
The same holds for the sixth and eighth octants.
-limit.
The same holds for the sixth and eighth octants.
