Electron. J. Differential Equations, Vol. 2020 (2020), No. 56, pp. 1-17.
Positive solutions for asymptotically 3-linear quasilinear Schrodinger equations
Guofa Li, Bitao Cheng, Yisheng Huang
Abstract:
In this article, we study the quasilinear Schrodinger equation
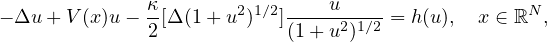
where
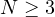 ,
,
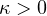 is a parameter,
is a parameter,
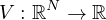 is a given potential. The nonlinearity
is a given potential. The nonlinearity
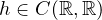 is asymptotically 3-linear at infinity. We obtain the nonexistence of a least energy
solution and the existence of a positive solution, via the Pohozaev manifold
and a linking theorem. Our results improve recent results in [4, 22].
is asymptotically 3-linear at infinity. We obtain the nonexistence of a least energy
solution and the existence of a positive solution, via the Pohozaev manifold
and a linking theorem. Our results improve recent results in [4, 22].
Submitted June 16, 2019. Published June 4, 2020.
Math Subject Classifications: 35J20, 35J62.
Key Words: Quasilinear Schrodinger equations; asymptotically 3-linear;
Pohozaev identity; linking theorem; positive solution.
DOI: 10.58997/ejde.2020.56
Show me the PDF file (378 KB),
TEX file for this article.
 |
Guofa Li
College of Mathematics and Statistics
Qujing Normal University
Qujing 655011, China
email liguofa2013@163.com
|
|---|
 |
Bitao Cheng
College of Mathematics and Statistics
Qujing Normal University
Qujing 655011, China
email: chengbitao2006@126.com
|
|---|
 |
Yisheng Huang
Department of Mathematics
Soochow University
Suzhou 215006, China
email: yishengh@suda.edu.cn
|
|---|
Return to the EJDE web page
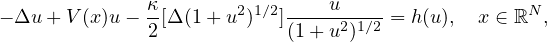
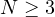 ,
,
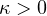 is a parameter,
is a parameter,
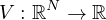 is a given potential. The nonlinearity
is a given potential. The nonlinearity
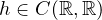 is asymptotically 3-linear at infinity. We obtain the nonexistence of a least energy
solution and the existence of a positive solution, via the Pohozaev manifold
and a linking theorem. Our results improve recent results in [4, 22].
is asymptotically 3-linear at infinity. We obtain the nonexistence of a least energy
solution and the existence of a positive solution, via the Pohozaev manifold
and a linking theorem. Our results improve recent results in [4, 22].


