Electron. J. Differential Equations, Vol. 2020 (2020), No. 68, pp. 1-25

Monotone iterative method for retarded evolution equations involving nonlocal and impulsive conditions

Xuping Zhang, Pengyu Chen, Yongxiang Li

Abstract:
In this article, we apply the perturbation technique and monotone iterative method in the presence of the lower and the upper solutions to discuss the existence of the minimal and maximal mild solutions to the retarded evolution equations involving nonlocal and impulsive conditions in an ordered Banach space X

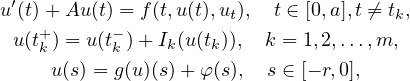
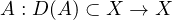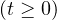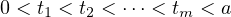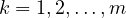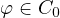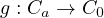where $A:D(A)\subset X\to X$ is a closed linear operator and -A generates a strongly continuous semigroup T(t) $(t\geq 0)$ on X, a, r>0 are two constants, $f:[0,a]\times X\times C_0\to X$ is Caratheodory continuous, $0<t_1<t_2<\dots<t_m<a$ are pre-fixed numbers, $I_k\in C(X,X)$ for $k=1,2,\dots,m$, $\varphi\in C_{0}$ is a priori given history, while the function $g:C_{a}\to C_{0}$ implicitly defines a complementary history, chosen by the system itself. Under suitable monotonicity conditions and noncompactness measure conditions, we obtain the existence of the minimal and maximal mild solutions, the existence of at least one mild solutions as well as the uniqueness of mild solution between the lower and the upper solutions. An example is given to illustrate the feasibility of our theoretical results.

Submitted August 11, 2019. Published July 1, 2020.
Math Subject Classifications: 35K90, 47D06, 47H08.
Key Words: Evolution equation; delay; impulsive function; nonlocal condition; iterative method; measure of noncompactness.
DOI: 10.58997/ejde.2020.68

Show me the PDF file (406 KB), TEX file for this article.

Xuping Zhang
Department of Mathematics
Northwest Normal University
Lanzhou 730070, China
email: lanyu9986@126.com
Pengyu Chen
Department of Mathematics
Northwest Normal University
Lanzhou 730070, China
email: chpengyu123@163.com
Yongxiang Li
Department of Mathematics
Northwest Normal University
Lanzhou 730070, China
email: liyx@nwnu.edu.cn}

Return to the EJDE web page